Анимация в matplotlib
Contents
Анимация в matplotlib#
Пример из руководства#
Коротко разберем, как можно осуществлять анимацию средствами matplotlib. Начнем с примера, приведенного в руководстве.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
fig, ax = plt.subplots()
xdata, ydata = [], []
ln, = plt.plot([], [], 'ro')
def init():
ax.set_xlim(0, 2*np.pi)
ax.set_ylim(-1, 1)
return ln,
def update(frame):
xdata.append(frame)
ydata.append(np.sin(frame))
ln.set_data(xdata, ydata)
return ln,
ani = FuncAnimation(fig, update, frames=np.linspace(0, 2*np.pi, 128),
init_func=init, blit=True)
plt.show()
Запуск скрипта с таким содержимым создаст окно, на котором постепенно построится график синуса. Есть как минимум два подхода заставить этот пример работать в jupyter notebook:
a) применить команду %matplotlib notebook, т.е. сделать что-то такое
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
%matplotlib notebook
Эта команда встраивает окна, созданные matplotlib, в выход ячейки, сохраняя интерактивность.
b) использовать специализированные средства jupyter ноутбуков для отображения анимации. Для этого надо заменить plt.show() на набор следующих команд
from IPython.display import HTML, display
display(HTML(animation.to_jshtml()))
plt.close(fig)
Метод to_jshtml генерирует html код, соответствующий анимации, функция HTML из модуля IPython.display обрабатывает html, а функция display отображает его. Метод plt.close используется чтобы скрыть созданную фигуру, т.к. она отображается в jupyter notebook по умолчанию, несмотря на то, что метод plt.show не вызывается.
Т.к. первый способ не отображается на этом ресурсе (приблизительно по той же причине, что графики plotly), то везде ниже будет использоваться второй способ.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
fig, ax = plt.subplots(figsize=(8, 6))
xdata, ydata = [], []
ln, = plt.plot([], [], 'ro')
def init():
ax.set_xlim(0, 2*np.pi)
ax.set_ylim(-1, 1)
return ln,
def update(frame):
xdata.append(frame)
ydata.append(np.sin(frame))
ln.set_data(xdata, ydata)
return ln,
animation = FuncAnimation(fig, update, frames=np.linspace(0, 2*np.pi, 128),
init_func=init, blit=True)
from IPython.display import HTML, display
display(HTML(animation.to_jshtml()))
plt.close(fig)
Вернемся к разбору этого примера.
Для создания анимации используется функция FuncAnimation из подмодуля matplotlib.animation, основными аргументами которой являются fig, blit, func, init_func, frames.
fig — фигура, которая будет использоваться для анимации. Функция FuncAnimation будет периодически обновлять содержимое этой фигуры, при этом она способна делать это экономно. Если передать в качестве параметра blit значение True, то содержимое фигуры перерисовывается не полностью, а обновляются лишь те компоненты (линия синуса в данном примере), которые изменяются между кадрами. За перерисовку кадра отвечает второй параметр func функции FuncAnimation, в качестве которого передается функция update в этом примере. Также есть опциональный параметр init_func (функция init в примере), который используется для подготовки фигуры перед началом анимации.
Рассмотрим подробнее последние два параметра func и init_func.
Если
blit==False, то действие функцииFuncAnimationгрубо можно описать в виде
...
init_func()
for f in frames:
func(f, *fargs)
...
...
Т.е. вначале вызывается функция init_func, после чего функция func вызывается с каждым значением из аргумента frames (*fargs можно передать в функцию FuncAnimation в качестве дополнительного параметра).
Если
blit==True, действие функцииFuncAnimationгрубо можно описать в виде
...
artists = init_func()
for f in frames:
artists = func(f, *fargs)
update_blit(artists)
...
...
В данном случае функции init_func и func должны возвращать artists — список (или любой другой итерируемый объект) элементов на графике, которые необходимо обновить.
fig, ax = plt.subplots(figsize=(8, 6))
xdata, ydata = [], []
ln, = plt.plot([], [], 'ro')
def init():
ax.set_xlim(0, 2*np.pi)
ax.set_ylim(-1, 1)
return ln,
def update(frame):
xdata.append(frame)
ydata.append(np.sin(frame))
ln.set_data(xdata, ydata)
return ln,
В рассматриваемом примере функция init задаёт диапазоны для горизонтальной и вертикальной осей графика, а функция update принимает на вход значение x, обновляет списки xdata и ydata, а затем обновляет и содержимое нарисованной линии ln графика синуса. При этом обе этих функции возвращают объект линии ln, чтобы функция FuncAnimation перерисовала этот объект.
Недостатком данного примера является тот факт, что функции init и update используют объекты из глобального пространства имен. Самый удобный способ избежать этого — создать пользовательский класс, чтобы инкапсулировать всё необходимое в один объект. Ниже приведен пример того, как это можно осуществить.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
class SinAnimation:
def __init__(self):
self.fig, self.ax = plt.subplots(figsize=(8, 6))
self.xdata = []
self.ydata = []
self.ln, = plt.plot([], [], 'ro')
def init_func(self):
self.ax.set_xlim(0, 2*np.pi)
self.ax.set_ylim(-1, 1)
return self.ln,
def update_func(self, frame):
self.xdata.append(frame)
self.ydata.append(np.sin(frame))
self.ln.set_data(self.xdata, self.ydata)
return self.ln,
painter = SinAnimation()
animation = FuncAnimation(
painter.fig,
painter.update_func,
frames=np.linspace(0, 2*np.pi, 128),
init_func=painter.init_func, blit=True)
from IPython.display import HTML, display
display(HTML(animation.to_jshtml()))
plt.close(painter.fig)
Объектно ориентированное программирование в python будет обсуждаться позже, а пока лишь коротко отметим основные детали.
class SinAnimation:заголовок объявления пользовательского класса с названиемSinAnimation. Далее следует объявление этого класса с отступом вправо;далее объявлены методы этого класса. У всех из них обязательным первым аргументом идёт имя
self— ссылка на текущий объект (аналогthisизC++);метод
__init__— конструктор класса, который вызывается при создании экземпляра класса. Создание экземпляра осуществляется в строкеpainter = SinAnimation();
Пример с математическим маятником#
Рассмотрим гармонические колебания математического маятника. Пусть \(\theta\) — отклонение маятника (угол) от положения равновесия, \(L\) — длина подвеса.
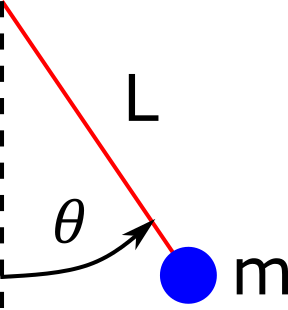
Тогда в случае малых колебаний
где \(A\) — амплитуда колебаний, \(\alpha\) — начальная фаза колебаний, а \(\omega_0\) — собственная частота колебаний.
Анимируем колебания такого маятника.
import numpy as np
import matplotlib.pyplot as plt
from matplotlib.animation import FuncAnimation
from scipy.constants import g
# Параметры маятника
L = 1 # длина (m)
M = 1 # масса (kg)
omega_0 = np.sqrt(g / L) # собственная частота
T = 2 * np.pi / omega_0 # период колебаний
A = np.pi / 4 # амплитуда
alpha = -A # начальная фаза
# параметры для отрисовки
frames_per_period = 36 # количество кадров на один период
delta = 0.1 # отступ
N_periods = 4 # Количество периодов
t_final = N_periods * T
N_frames = frames_per_period * N_periods # итоговое количество кадров
def angle(t):
return A * np.sin(omega_0 * t + alpha)
def x_and_y(theta):
x = np.sin(theta)
y = L - L * np.cos(theta)
return x, y
class PendulumAnimation:
def __init__(self):
self.t = np.linspace(0, t_final, N_frames)
self.frames = np.arange(N_frames)
self.theta = angle(self.t)
self.x, self.y = x_and_y(self.theta)
self.fig, self.ax = plt.subplots(figsize=(8, 8))
self.delta = 0.05
self.trace, = plt.plot([self.x[0]], [self.y[0]], 'bo-', lw=1, ms=2)
self.l, = plt.plot([0], [1], 'bo-', lw=4, ms=15)
def init(self):
# limits
x_min, x_max = self.x.min(), self.x.max()
y_min, y_max = self.y.min(), self.y.max()
self.ax.set_xlim([-L - delta, L + delta])
self.ax.set_ylim([0 - delta, 2 * L + delta])
self.ax.set_xlabel("x")
self.ax.set_ylabel("y")
return self.l, self.trace
def update(self, frame):
xs = [0, self.x[frame]]
ys = [1, self.y[frame]]
self.trace.set_data(self.x[:frame], self.y[:frame])
self.l.set_data(xs, ys)
return self.l, self.trace
painter = PendulumAnimation()
animation = FuncAnimation(
painter.fig,
painter.update,
frames=painter.frames,
init_func=painter.init,
blit=False,
interval=T / frames_per_period * 1000
)
from IPython.display import HTML, display
display(HTML(animation.to_jshtml()))
plt.close(painter.fig)
Функция angle(t) задаёт зависимость угла \(\theta\) от времени \(t\), а функция x_and_y(theta) определяет положение маятника в декартовых координатах \(xOy\) при заданном угле \(\theta\).
Анимирование маятника осуществляется с помощью обычного графика с увеличенными маркерами (параметр ms, сокращение от marker size). Отрисовка в целом не сильно отличается от предыдущих примеров за исключением того, что необходимо корректно подобрать частоту кадров (fps) в анимации (или длину интервала между ними), т.к. визуализируется реальная физическая система.


