Домашнее задание №1

В рамках первого домашнего задания от вас требуется:

1. Установить python;

2. Установить среду разработки на вкус;

3. Реализовать один из численных методов описанных ниже.

Метод и функция, для которой его необходимо применить в обязательном порядке, определяются вариантом, которые перечисленны ниже.

Варианты

Вариант №	Метод	\(f(x)\)
1	Бисекции	\(\ln x - \dfrac{1}{x}\)
2	Хорд	\(e^x + x\)
3	Ньютона	\(\dfrac{1}{x} - 2x\)
4	Золотого сечения	\(\log (\lvert x \rvert+1)\)
5	Градиентного спуска	\(\tanh x + x^2\)
6	Бисекции	\(\log x + 1\)
7	Хорд	\(\arctan x - \dfrac{1}{2}\)
8	Ньютона	\(e^x - \dfrac{1}{2}\)
9	Золотого сечения	\(\lvert x-1\rvert + x^2\)
10	Градиентного спуска	\(x^2 + 2x - 3\)
11	Бисекции	\(\tan 2x - 1 - x\)
12	Хорд	\(2e^{-x} - x\)
13	Ньютона	\(e^{-3x^2} - x\)
14	Золотого сечения	\(e^{\lvert x-1\rvert} - x^2\)
15	Градиентного спуска	\(\cosh x + x\)
16	Бисекции	\(e^{-3x} + 1 - x\)
17	Хорд	\(e^{-x^2} - x\)
18	Ньютона	\(e^{-x^2} - x^2\)
19	Золотого сечения	\(e^{-x^2}\)
20	Градиентного спуска	\(\arctan x + x^2\)
21	Бисекции	\(3e^{-3x} - x\)
22	Хорд	\(e^{-x^3} - 1 - x^3\)
23	Ньютона	\(2e^{-3x} + 1 - x\)
24	Золотого сечения	\(\sinh(\lvert x\rvert+1) - x^2\)
25	Градиентного спуска	\(-\arctan e^{-x^2}\)

Численные методы поиска минимума или корня скалярной функции

В рамках первого домашнего задания от вас потребуется реализовать численный метод поиска корня уравнения вида

(1)\[f(x) = 0,\]

или численный метод поиска минимума скалярной функции \(f\):

(2)\[f(x) \sim \min_{x \in X}.\]

В обоих случаях \(f\) — скалярная функция одного аргумента, т.е. \(f\colon \mathbb{R} \to \mathbb{R}\).

Это задание нацелено в первую очередь на освоение синтаксиса языка python, поэтому ниже приводится подробное описание алгоритмов работы каждого метода, а вам предлагается реализовать один из них средствами python. К вашему решению предъявляются следующие требования:

1. Решение должно быть оформлено в виде скрипта python (файл с расширением “.py”, а не блокнот jupyter)!

2. Ввод параметров должен осуществляться пользователем средствами стандартного потока ввода.

3. Численный метод должен быть оформлен в виде отдельной процедуры (python функции).

4. Введенные пользователем данные должны передаваться процедуре численного метода в качестве аргументов.

5. Процедура численного метода должна возвращать найденный корень или минимум, если алгоритм сошелся, и значение None, если алгоритм не применим или разошелся.

6. Реализованный метод должен печатать отладочную информацию в стандартный поток вывода.

7. Реализованный метод поиска корня должен быть протестирован на каких-то простых примерах.

Tip

Ваш численный метод так или иначе должен будет вызывать функцию \(f\) и/или \(f'\) внутри себя на каждой итерации, чтобы двигаться в сторону корня или минимума.

Самый простой способ этого добиться — определить функцию \(f(x)\) (и/или \(f'(x)\)) глобально и тогда на неё можно будет ссылаться внутри вашего метода. Хотя такое решение и будет приниматься преподавателем, оно не является идеальным: такая реализация ищет корень одной конкретной функции \(f(x)\), а для того, чтобы найти корень любой другой функции, придется модифицировать исходный код.

Более гибкое решение подразумевает передачу искомой функции \(f(x)\) (и/или \(f'(x)\)) в качестве аргумента в метод поиска корня. В python функции можно передавать в качестве аргументов другим функциям точно также, как и любые другие переменные (иными словами функции в python — объекты первого класса).

Метод бисекции

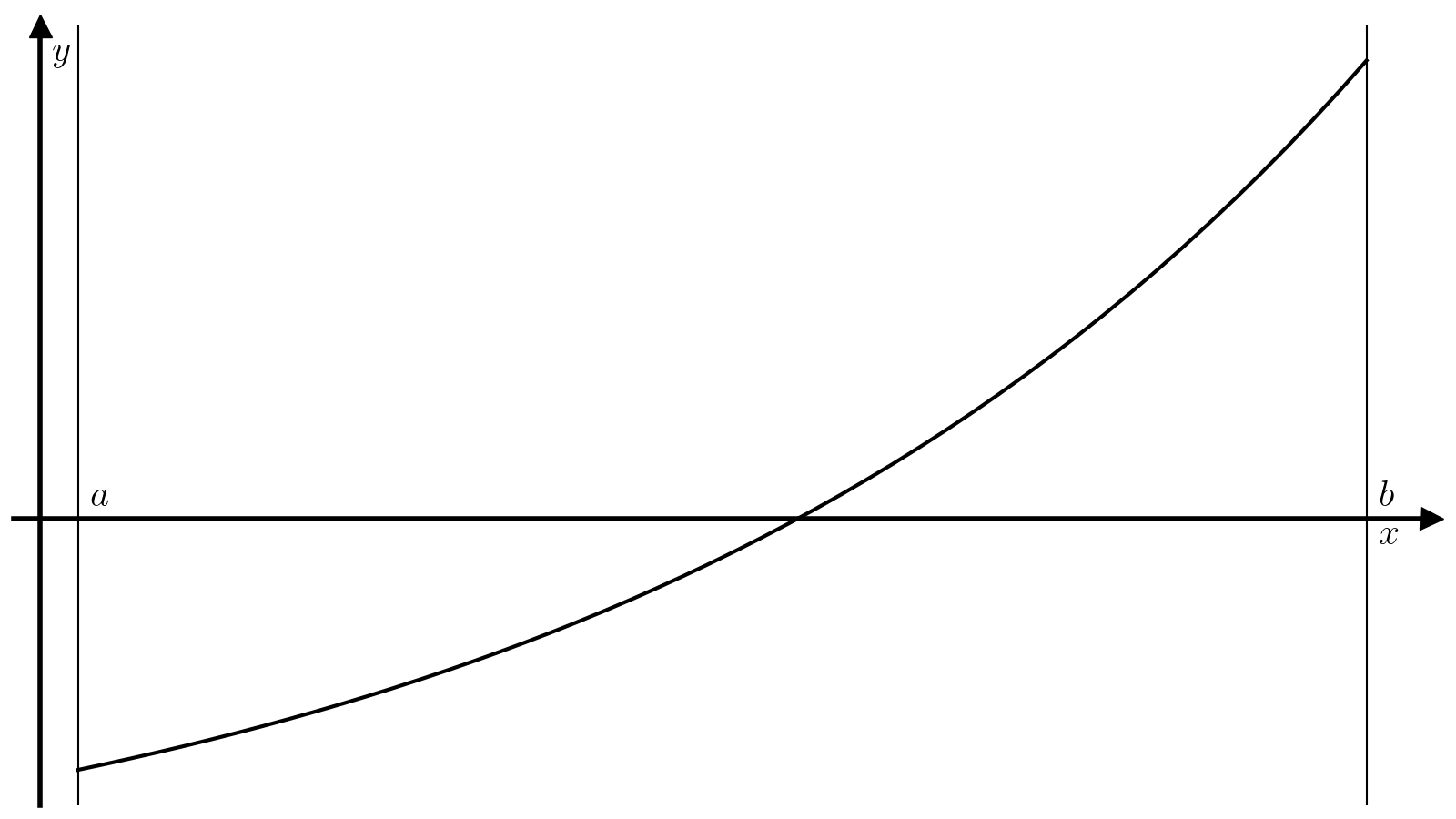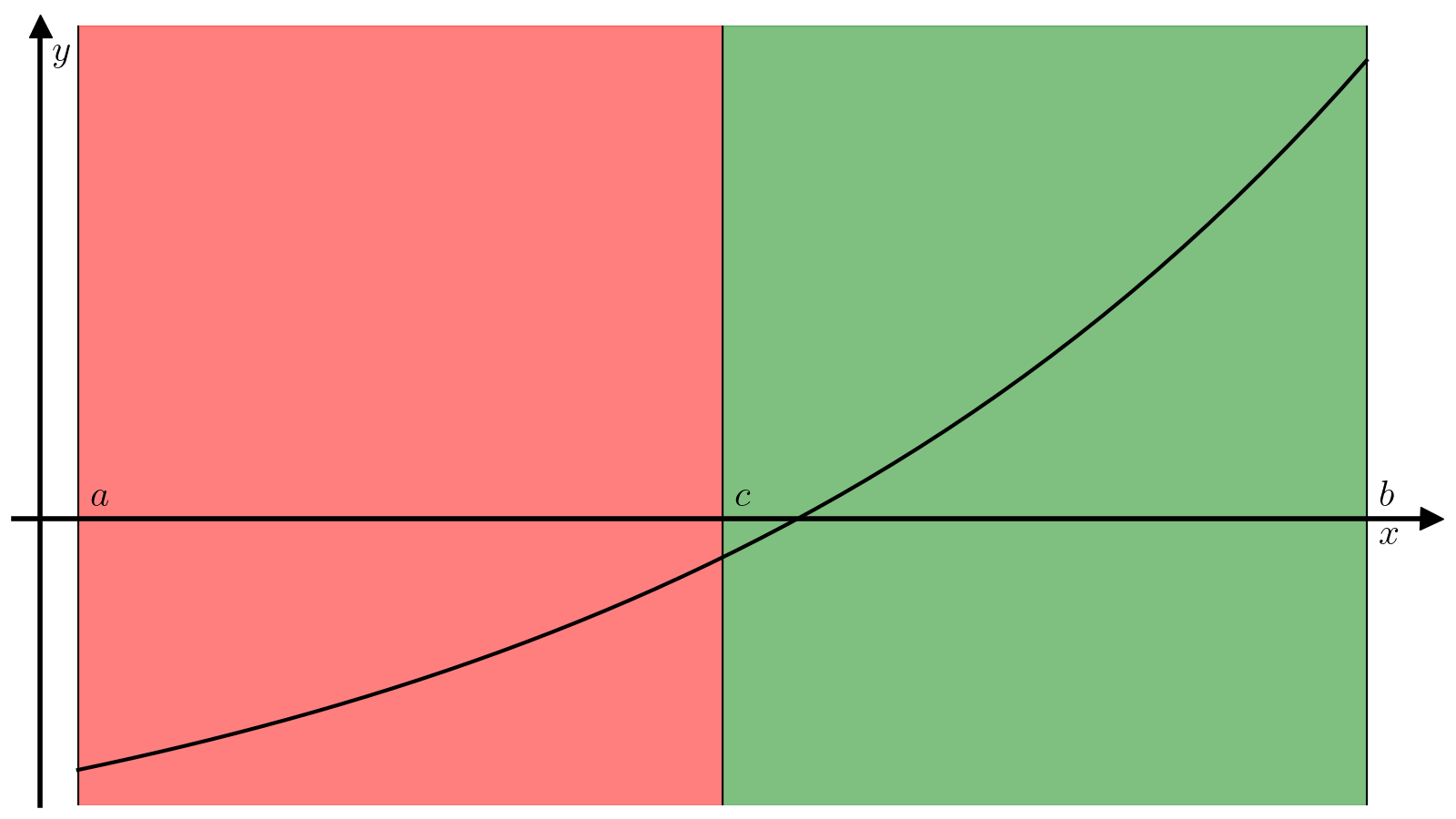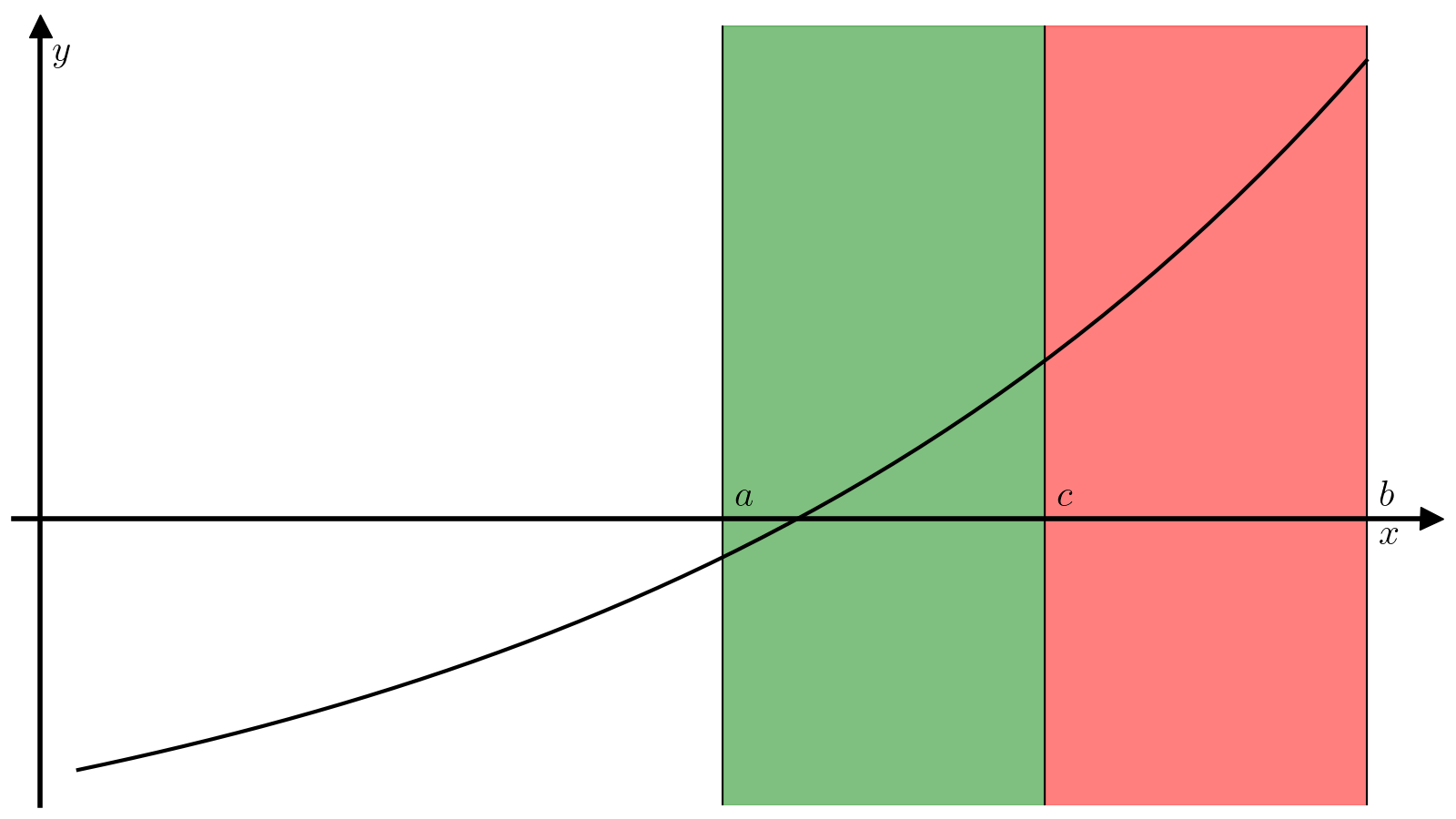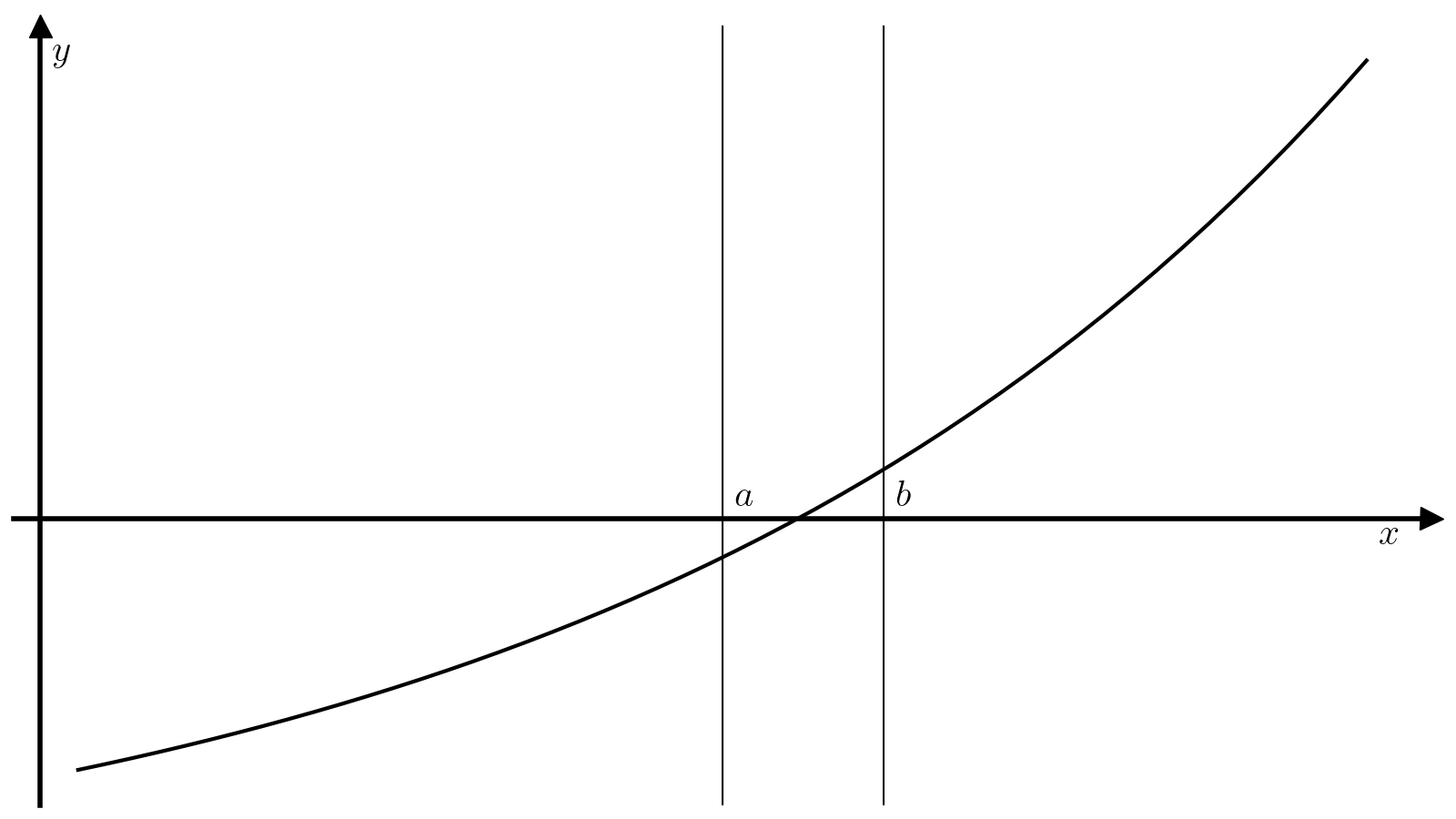
Метод бисекции — один из самых примитивных методов решения уравнений вида (1), который ищет корень непрерывной на некотором отрезке \([a, b]\) функции. Для работы этого метода требуется, чтобы значение функции \(f\) на концах отрезка \([a, b]\) были разного знака:

(3)\[f(a)f(b)<0. \]

Тогда из теоремы о промежуточном значении следует, что найдется минимум один корень функции \(f\) на отрезке \([a, b]\), а метод бисекции позволяет найти этот корень с произвольной точностью.

Основная идея алгоритма поиска корня методом бисекции заключается в следующем. Поделим отрезок \([a, b]\) пополам, т.е. найдем точку \(c\):

(4)\[c = \dfrac{a + b}{2}.\]

В зависимости от значения величины \(f(c)\), реализуется один из следующих вариантов.

• \(f(c) = 0\), т.е. уравнение (1) решено и \(c\) — его корень;

• \(f(c) f(a) < 0\), т.е. можно продолжить поиск корная на отрезке \([a, c]\);

• \(f(c) f(a) > 0\), а значит \(f(c) f(b) < 0\) и можно продолжить поиск корня на отрезке \([c, b]\).

Итого, с помощью одного такого шага мы или найдем корень, или сузим вдвое длину отрезка, на котором ищется корень. Обычно такие шаги применяют многократно до тех пор, пока не будет достигнута необходимая точность (длина отрезка \([a, b]\)) и невязка (модуль значения функции \(|f(c)|\)), т.е. критерием сходимости метода является одновременное выполнение двух условий

\[\begin{split} \begin{cases} |b - a| < \delta, \\ |f(c)| < \varepsilon. \end{cases} \end{split}\]

Пусть заданы требуемые точность delta и невязка epsilon. Тогда алгоритма поиска минимума корня функции f на отрезке [a, b] методом бисекции состоит из следующих шагов.

1. Проверить выполнение условия (3). Если условие не выполняется, то решения на заданном интервале нет, либо оно не единственно. Работа алгоритма немедленно завершается. Если условие выполняется, то перейти к следующему шагу.

2. Найти середину отрезка c по формуле (4).

3. Проверить выполнение критериев остановки. Если |f(c)| < epsilon и |b-a|< delta, то принять, что c — искомый корень и работа алгоритма прекращается немедленно. Иначе перейти к следующему шагу.

4. Проверить, на каком из двух отрезков [a, c] или [c, b] функция меняет знак. Если f(a) f(c) < 0, то b = c. Иначе, a = c. Вернуться к шагу №2.

Метод хорд

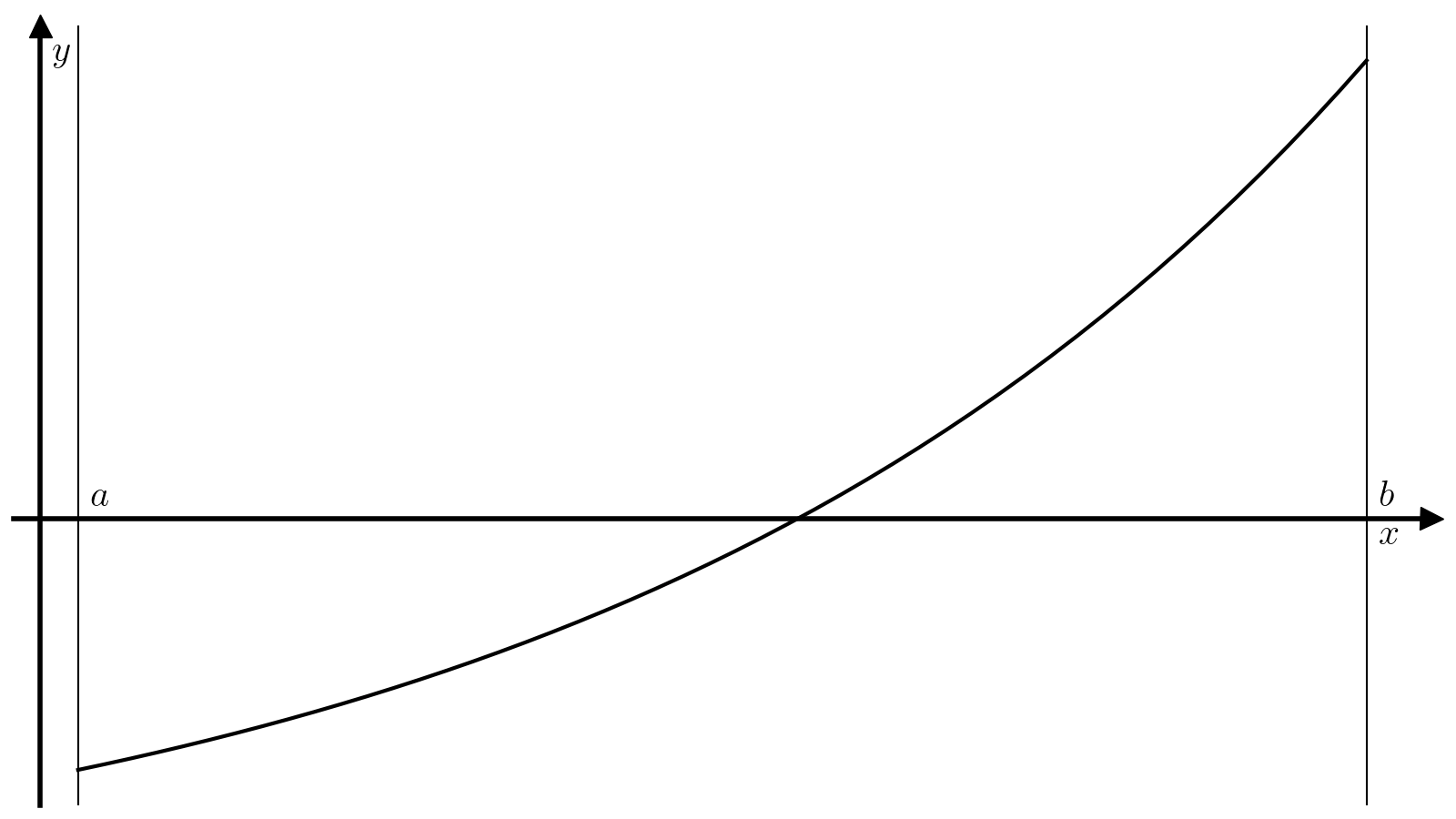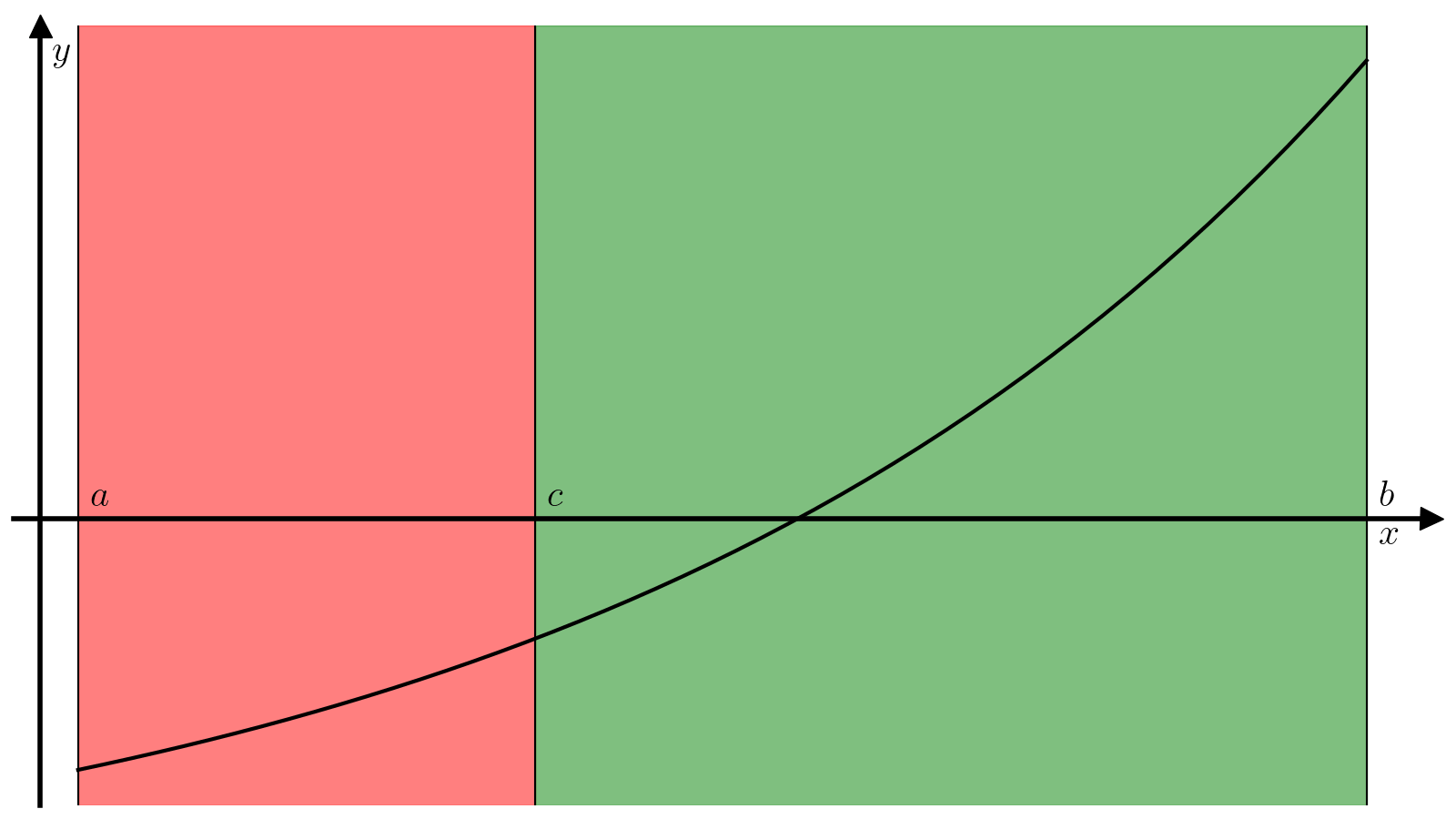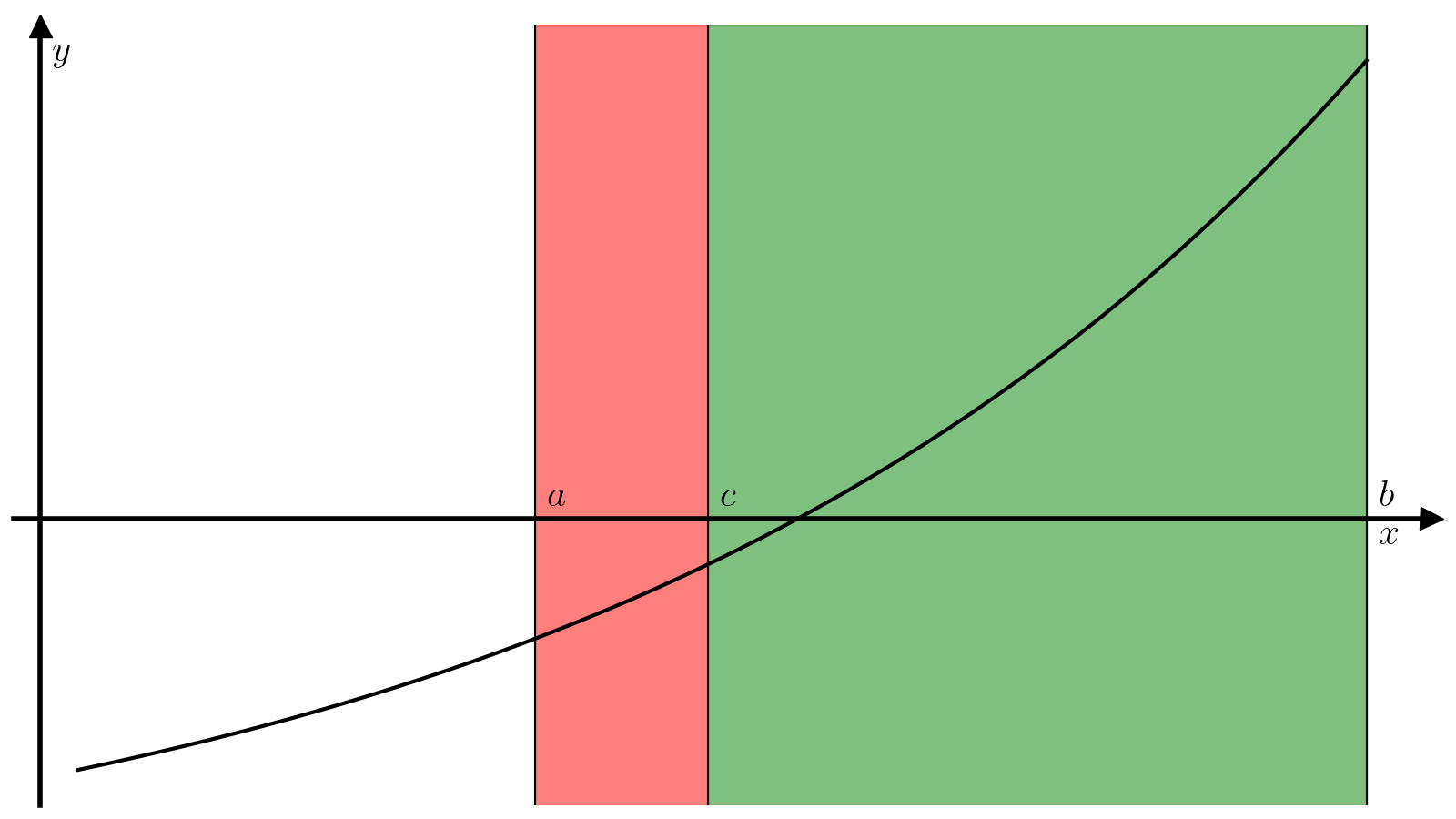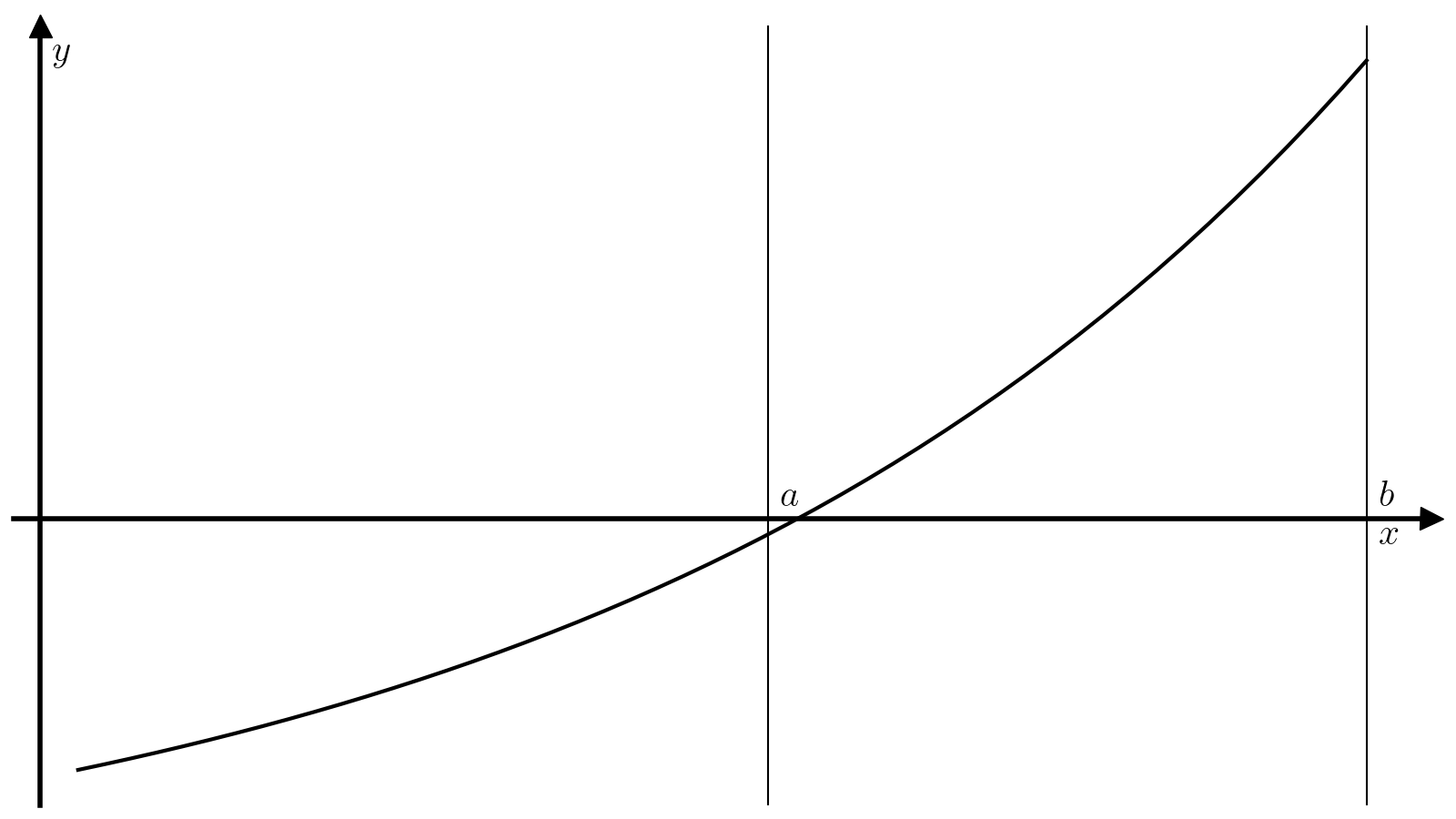
Идея метода хорд очень похожа на идею метода бисекции. Корень тоже ищется на отрезке \([a, b]\), на концах которого непрерывная функция \(f\) должна иметь разные знаки.

(5)\[f(a)f(b)<0. \]

На каждой итерации отрезок тоже делится на две части, но не пополам, а по следующей схеме. Через точки \((a, f(a))\) и \((b, f(b))\) проводится прямая

\[ y = f(a) \dfrac{x - b}{a - b} + f(b) \dfrac{a - x}{a - b}, \]

которую называют хордой или секущей. Эта прямая пересекает ось абсцисс в точке

(6)\[c = a - \dfrac{f(b)(b-a)}{f(b) - f(a)} \in (a, b),\]

которая определяет деление отрезка \([a, b]\) на два отрезка меньшей длинны: \([a, c]\) и \([c, b]\). Если точка \(c\) сама по себе не является корнем, то поиск продолжается на одном из двух этих отрезков. Обычно такие шаги применяют многократно до тех пор, пока не будет достигнута необходимая точность (длина отрезка \([a, b]\)) и невязка в средней точке (модуль значения функции \(|f(c)|\)), т.е. критерием сходимости метода является одновременное выполнение двух условий

\[\begin{split} \begin{cases} |b - a| < \delta, \\ |f(c)| < \varepsilon. \end{cases} \end{split}\]

Пусть заданы требуемые точность delta и невязка epsilon. Тогда алгоритма поиска минимума корня функции f на отрезке [a, b] методом хорд состоит из следующих шагов.

1. Проверить выполнение условия (5). Если условие не выполняется, то решения на заданном интервале нет, либо оно не единственно. Работа алгоритма немедленно завершается. Если условие выполняется, то перейти к следующему шагу.

2. Найти точку c по формуле (6).

3. Проверить выполнение критериев остановки. Если |f(c)| < epsilon и |b-a|< delta, то принимается, что c — искомый корень и работа алгоритма прекращается немедленно. Иначе, перейти к следующему шагу.

4. Выяснить, на каком из двух отрезков [a, c] или [c, b] функция меняет знак. Если f(a) f(c) < 0, то b = c. Иначе, a = c. Вернуться к шагу №2.

Метод Ньютона

Метод касательных (он же метод Ньютона) накладывает дополнительные требования на функцию \(f\): кроме непрерывности самой функции \(f\) требуется и непрерывность производной \(f'\). Другое отличие заключается в виде начального приближения: предыдущие два методы требовали отрезок, а метод Ньютона всего одну точку.

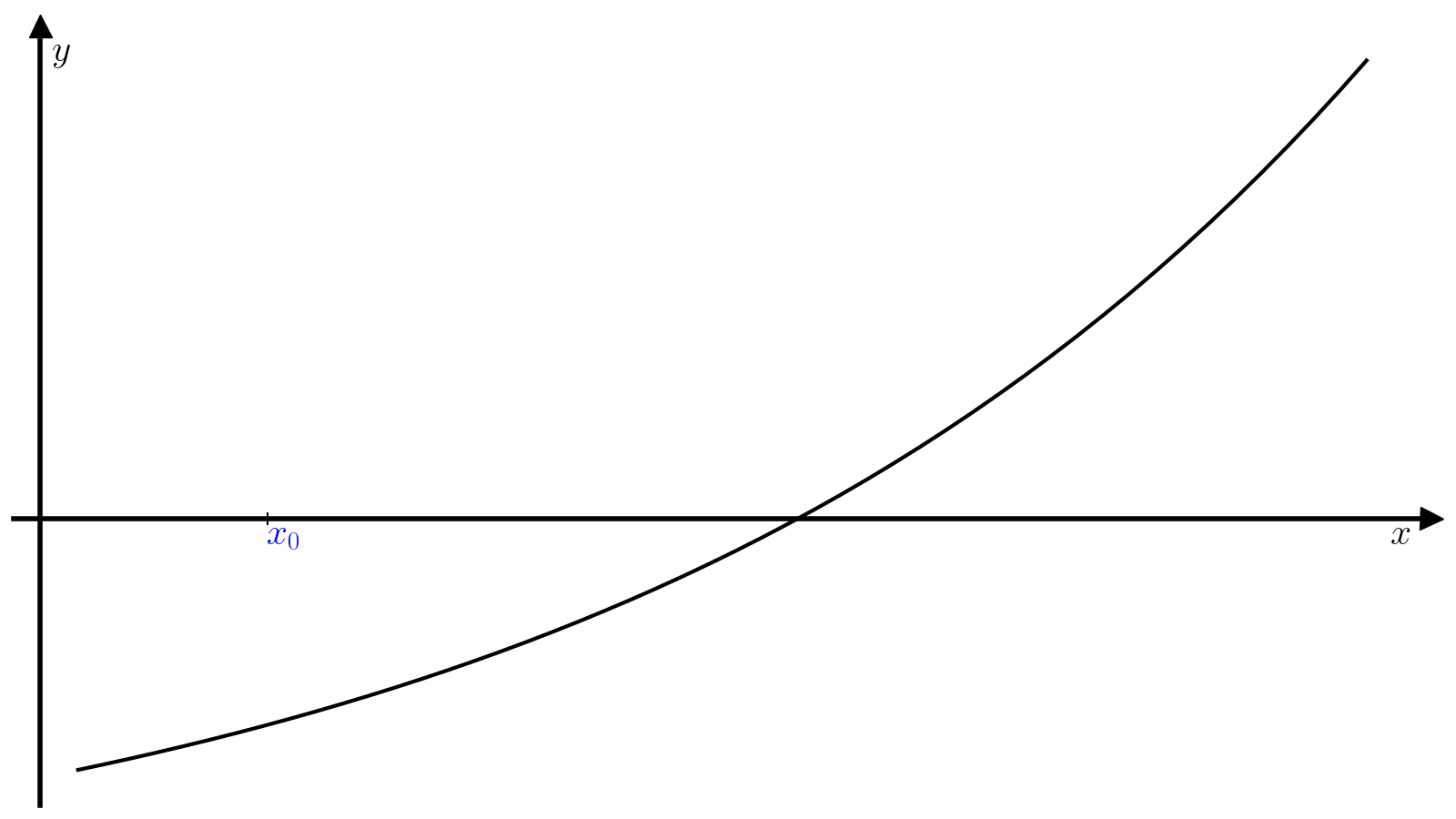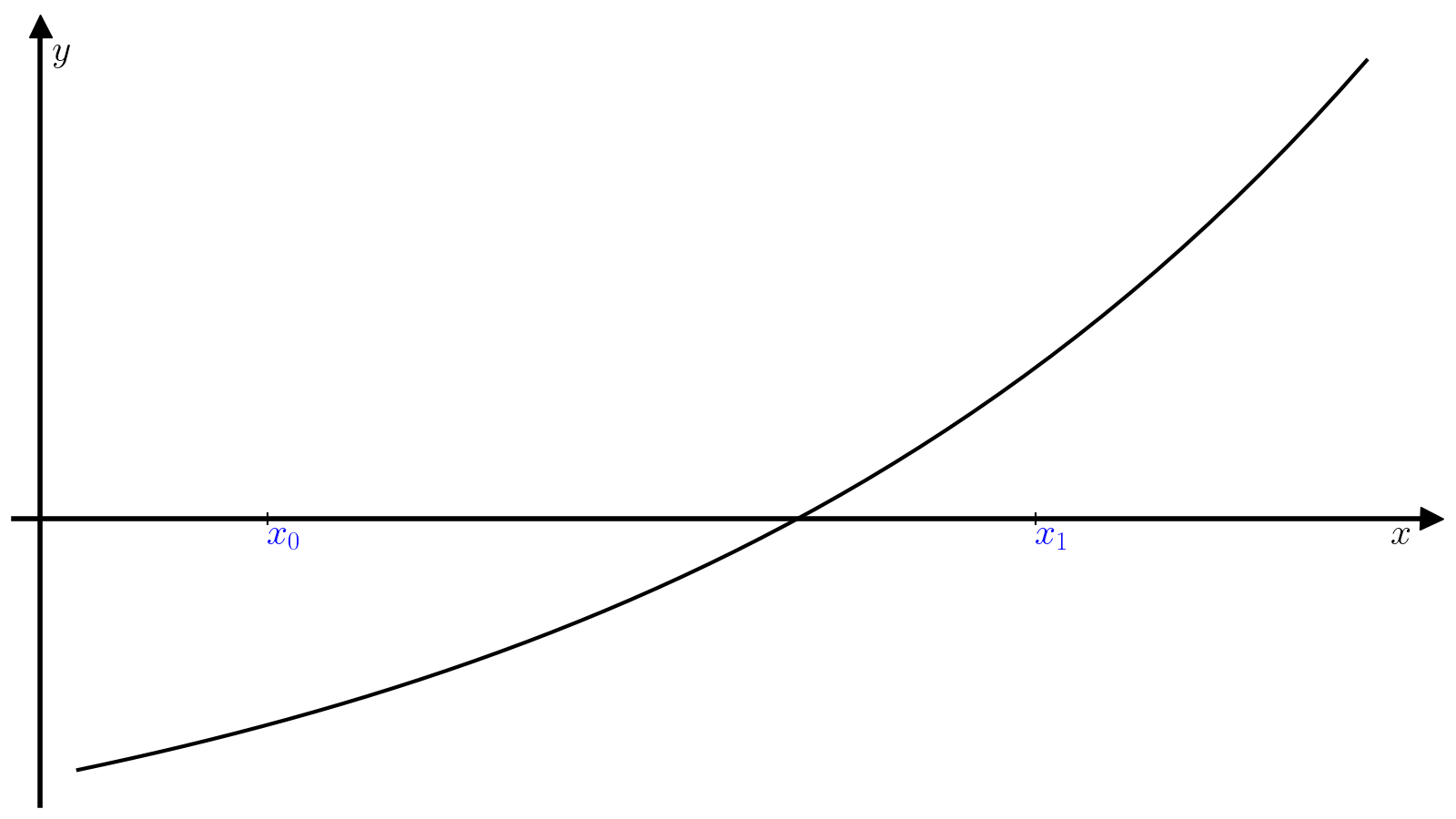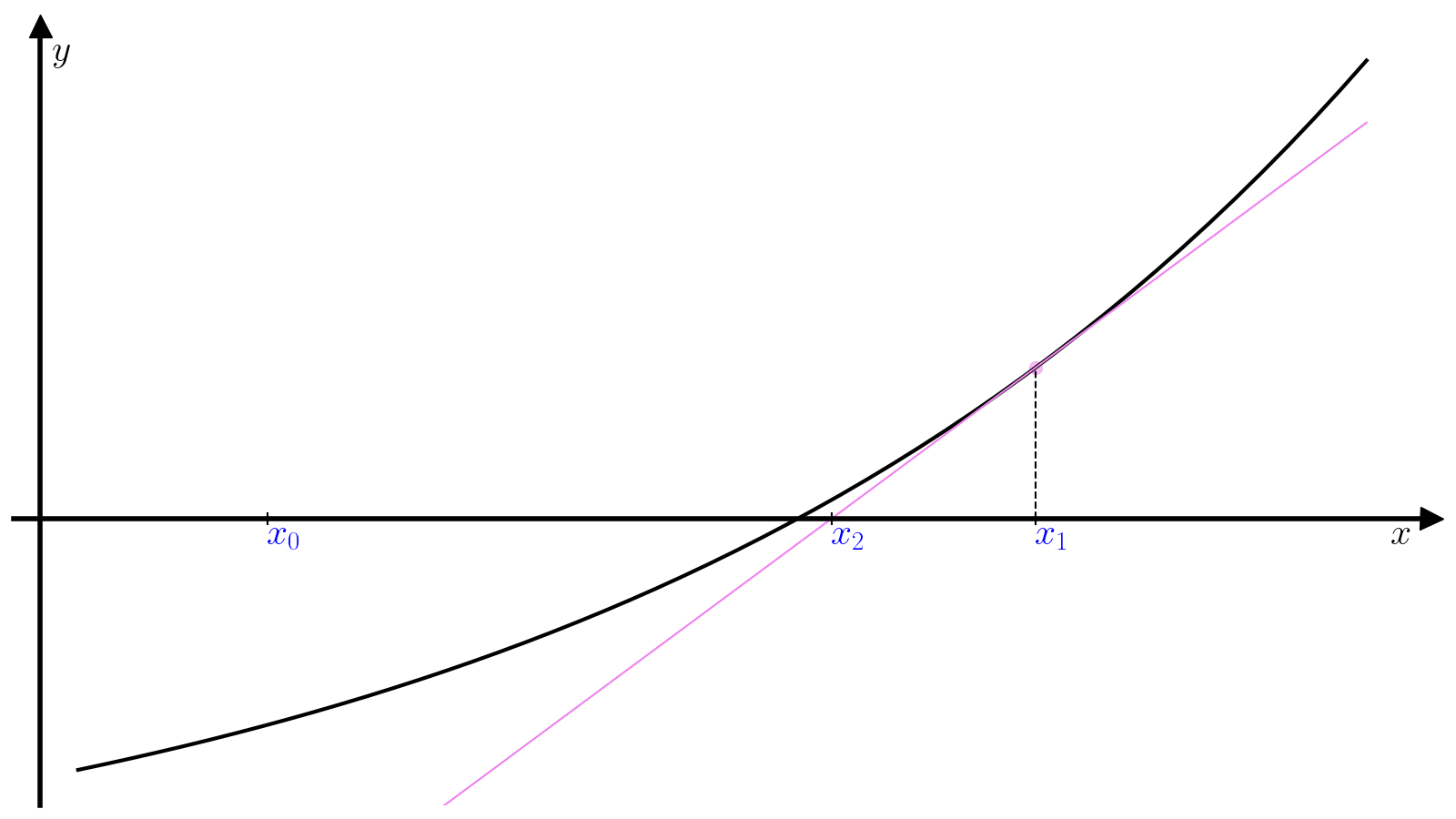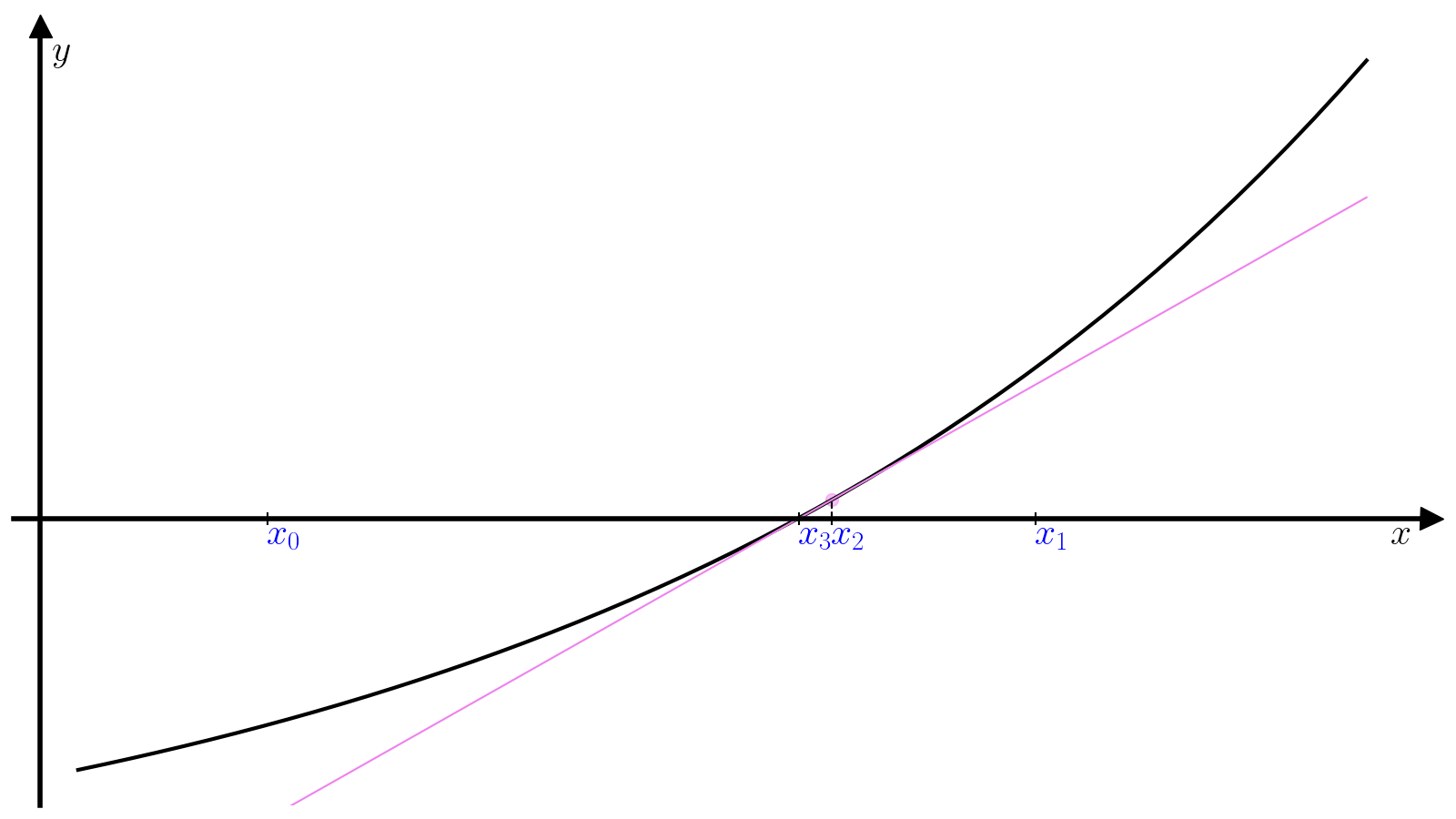
Пусть задано начальное приближение \(x_0\). Идея метода Ньютона заключается в том, чтобы аппроксимировать кривую \(f(x)\) касательной в окрестности точки \(x_0\) и найти следующее приближение \(x_1\) к корню функции \(f(x)\) как пересечение этой касательной с осью абсцисс. Касательная \(\hat{f}\) к функции \(f\) в точке \(x_0\) определяется уравнением

\[\hat{f}(x) = f'(x_0)(x - x_0) + f(x_0),\]

а координата \(x_1\) её точки пересечения с осью абсцисс выражением

\[x_1 = x_0 - \dfrac{f(x_0)}{f'(x_0)}.\]

Далее \(x_1\) используется в качестве начального приближения на следующей итерации, чтобы найти \(x_2\) и так далее.

(7)\[x_{i+1} = x_{i} - \dfrac{f(x_i)}{f'(x_i)}.\]

Условием сходимости является достаточная близость нулевого приближения \(x_0\) к корню. Гарантировать требуемую точность на каждой конкретной итерации не представляется возможным, поэтому погрешность обычно оценивают как величину \(|x_{i+1} - x_i|\), т.е. критерием сходимости является выполнение условий

\[\begin{split} \begin{cases} |x_{i + 1} - x_i| < \delta, \\ |f(x_{i+1})| < \varepsilon. \end{cases} \end{split}\]

Так как метод Ньютона может разойтись, если приближение далеко от корня, то кроме контроля невязки и точности требуется ограничивать максимальное количество итераций, чтобы исключить возможность попадания в бесконечный цикл.

Пусть заданы требуемые точность delta, невязка epsilon, максимальное количество итераций max_iter и начальное приближение x0. Тогда алгоритма поиска корня функции f методом Ньютона состоит из следующих шагов.

1. Инициализировать счетчик iter нулевым значением, а переменную x_previous значением x0.

2. Вычислить следующее приближение x_next на основе предыдущего x_previous по формуле (7).

3. Если |x_next - x_previous| < delta и f(x_next) < epsilon, то принять, что x1 — искомый корень и работа алгоритма прекращается немедленно. Иначе, перейти к шагу №4.

4. Если iter == max_iter, то принять, что алгоритм Ньютона разошелся и работа алгоритма прекращается немедленно. Иначе, перейти к шагу №5.

5. Присвоить переменной x_previous значение переменной x_next, увеличить счетчик iter на 1 и вернуться к шагу №2.

Метод дихотомии (метод золотого сечения)

Метод дихотомии предназначен для поиска минимумов унимодальной функции. Непрерывная функция \(f\colon \mathbb{R} \to \mathbb{R}\) называется унимодальной на отрезке \([a, b]\), если \(\exists! c \in [a, b]\), такая, что:

1. \(c\) — глобальный минимум функции \(f\), т.е. \(f(c) = f_* = \min\limits_{x\in[a, b]} f(x)\);

2. функция \(f\) монотонно убывает на отрезке \([a, c]\);

3. функция \(f\) монотонно растёт на отрезке \([c, b]\);

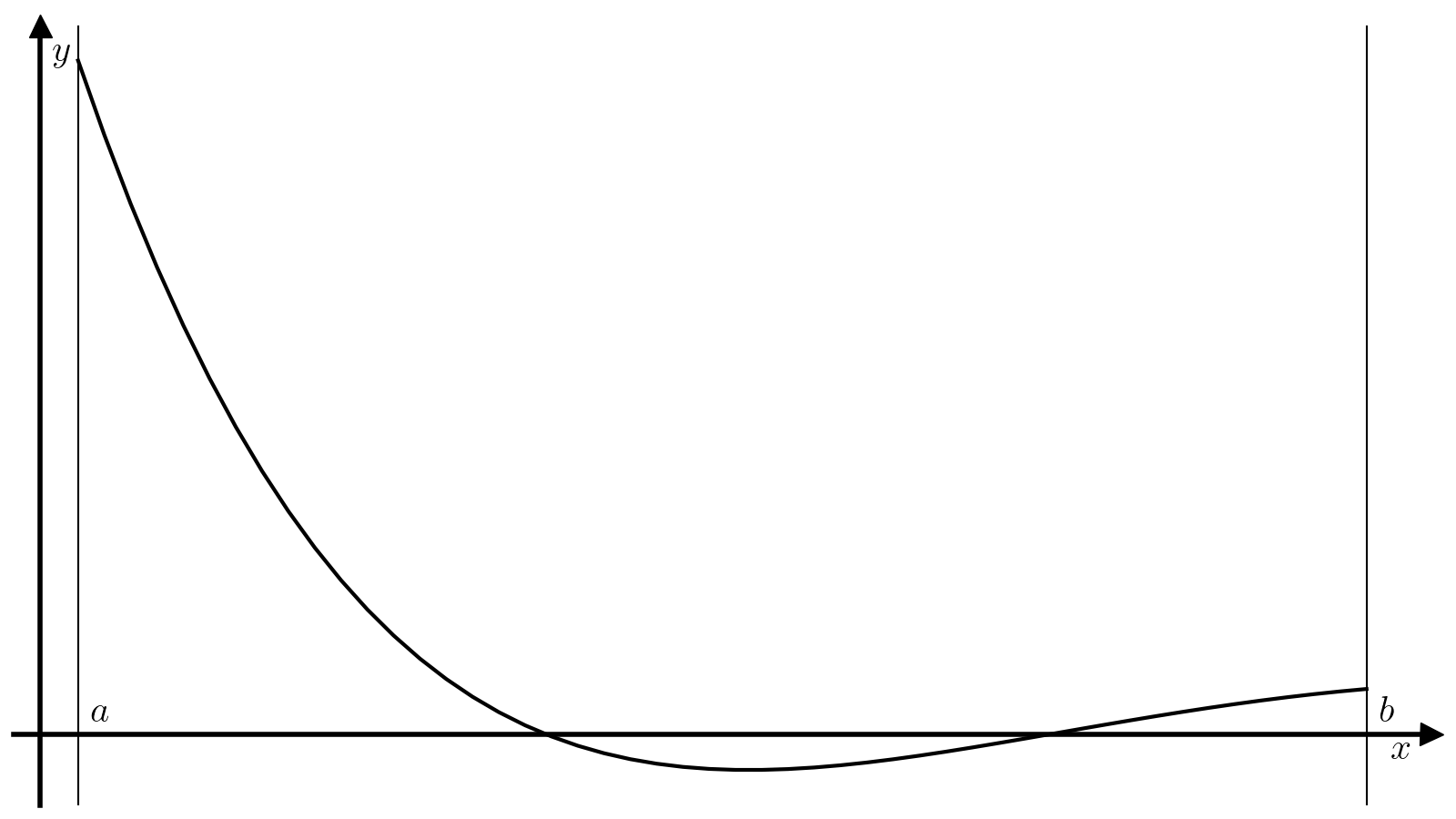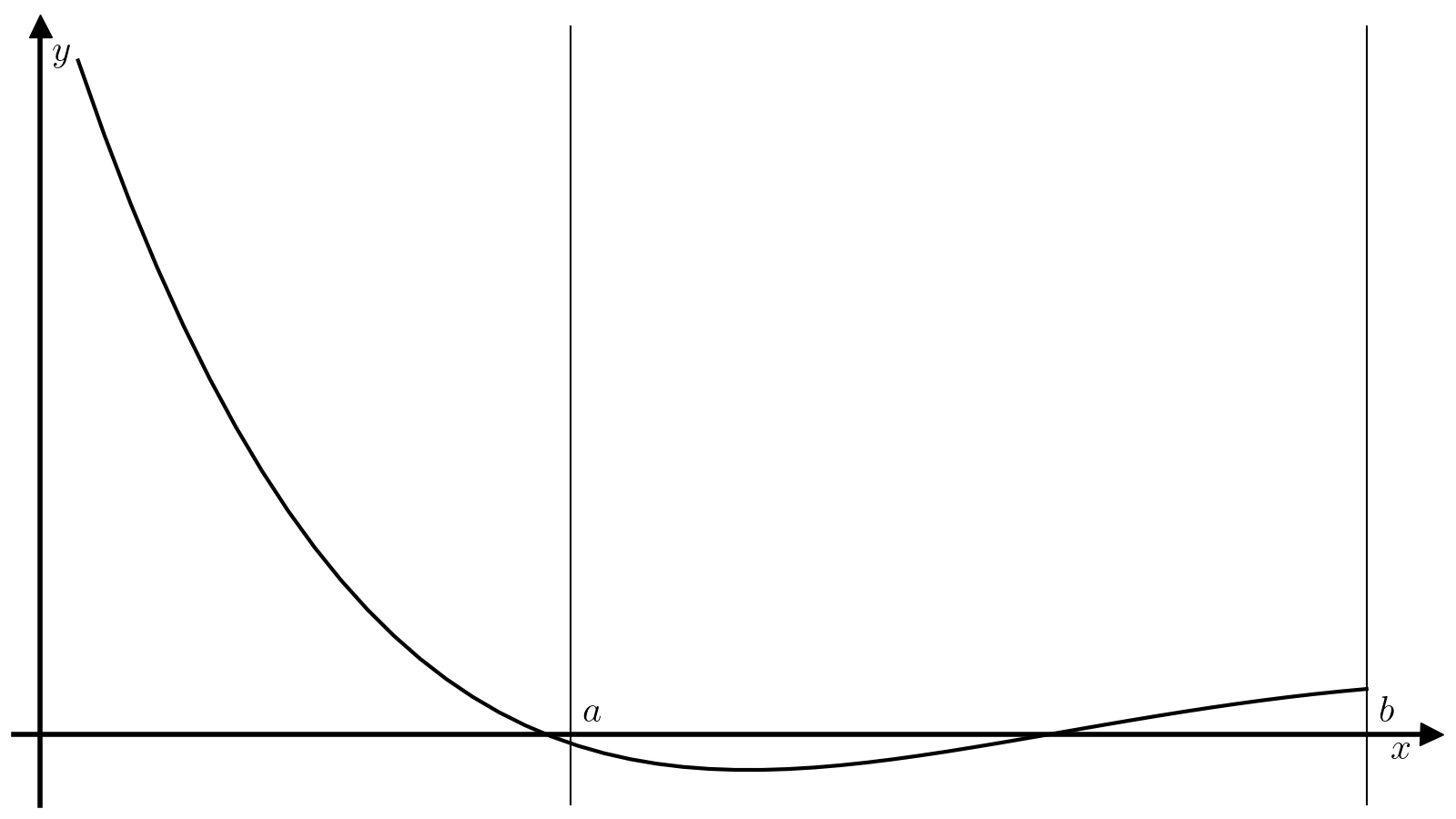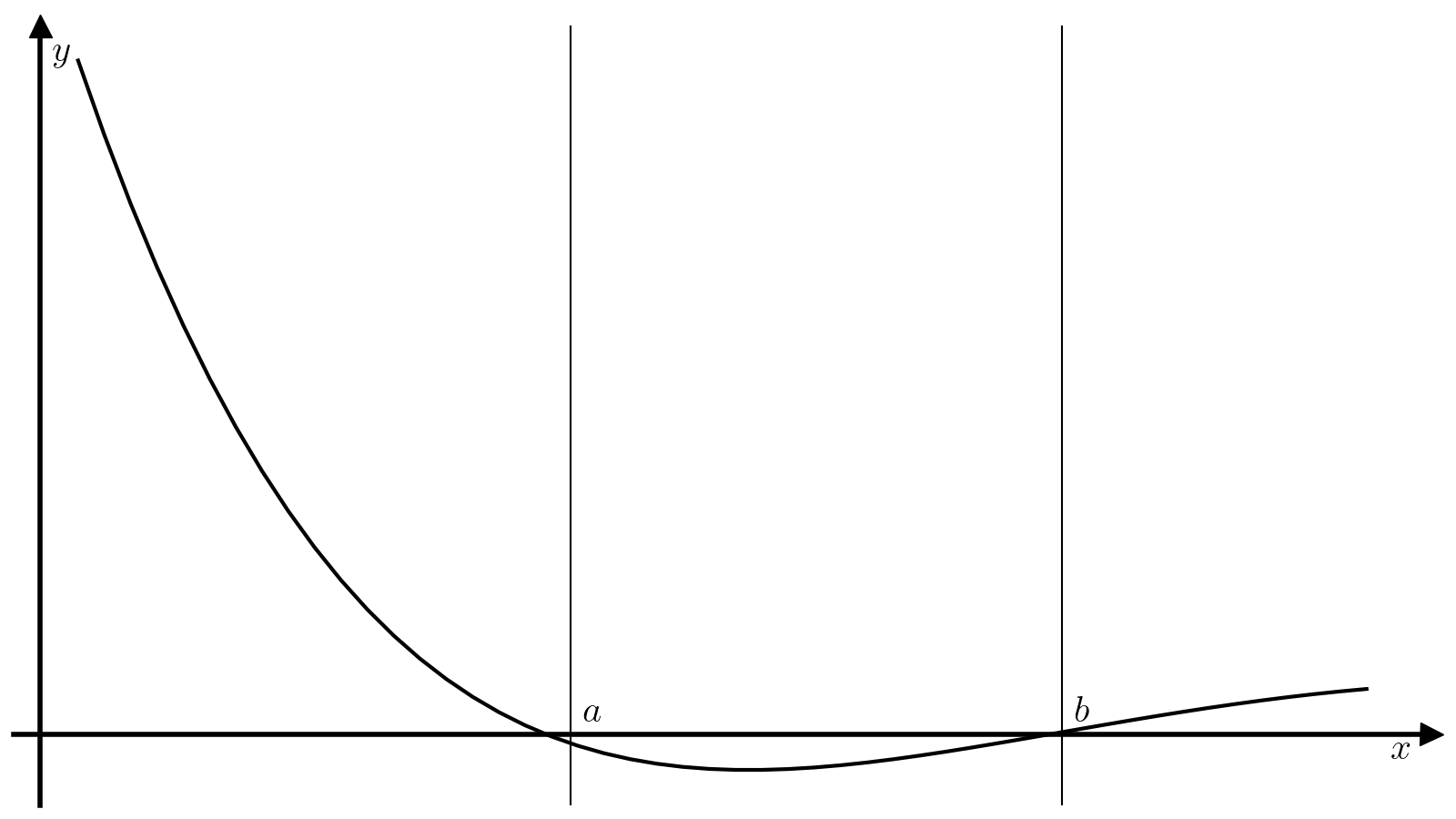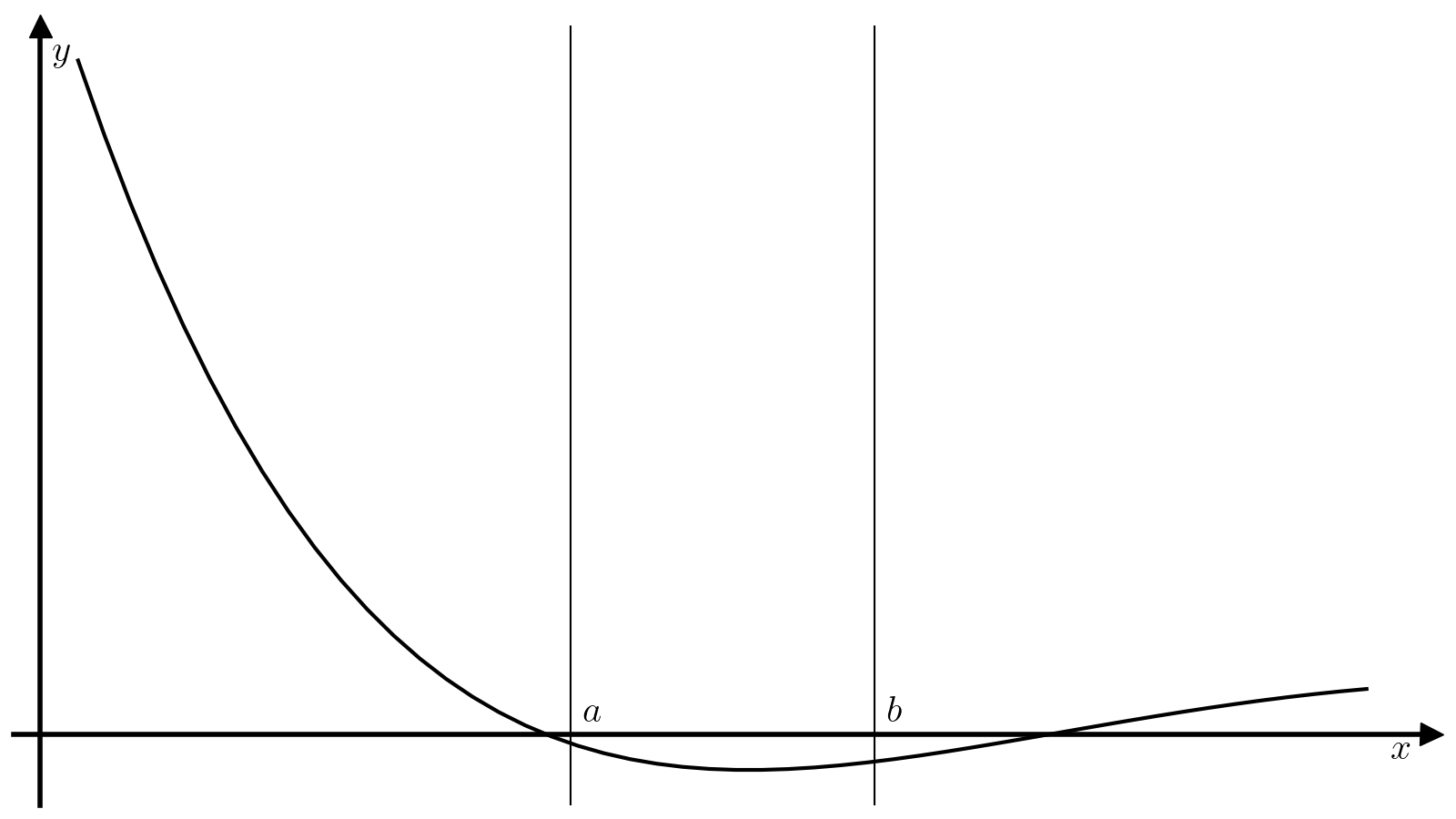
Унимодальная функция имеет ровно один локальный минимум, который одновременно является и единственным глобальным. Идея метода дихотомии основывается на том, что если \(f\) унимодальна на отрезке \([a, b]\), то разбив отрезок \([a, b]\) двумя точками \(x_1\) и \(x_2\), \(x_1 < x_2\), можно легко уточнить положение минимума функции \(f\):

• Если \(f(x_1) > f(x_2)\), то минимум достигается на отрезке \([x_1, b]\). Действительно, на отрезке \([c, b]\) функция \(f\) монотонно растет по определению, а значит \(x_1\) не может находиться внутри отрезка \([c, b]\), так как \(f(x_2) < f(x_1)\) при том, что \(x_2 > x_1\). Единственная альтернатива — \(x_1\in[a, c]\), т.е. минимум достигается на отрезке \([x_1, b]\).

• Если \(f(x_1) < f(x_2)\), то минимум достигается на отрезке \([a, x_2]\).

Note

Корректное определение унимодальной функции подразумевает несколько более общее определение, в котором точка минимума \(c\) как бы превращается в отрезок \([c_1, c_2]\), каждая точка которого является глобальным минимумом. Описанный здесь метод дихотомии сходится и для таких функций.

После сужения отрезка \([a, b]\) до \([x_1, b]\) или \([a, x_2]\) можно повторить процедуру деления отрезка на три части произвольное количество раз до достижения необходимой точности. За точность принимается длинна отрезка \([a, b]\) (величина \(b - a\)), т.е. критерием сходимости алгоритма считается выполнение условия

\[ |b - a| < \delta. \]

Метод золотого сечения — частный, который предписывает выбирать \(x_1\) и \(x_2\) по формулам

(8)\[\begin{split}\begin{cases} x_1 = \dfrac{a + b}{2} - (b - a)(\dfrac{1}{\Phi} - \dfrac{1}{2}), \\ x_2 = \dfrac{a + b}{2} + (b - a)(\dfrac{1}{\Phi} - \dfrac{1}{2}), \end{cases}\end{split}\]

где \(\Phi = \dfrac{1 + \sqrt{5}}{2}\) — золотое сечение. Выбор \(x_1\) и \(x_2\) позволяет на каждой следующей итерации вычислять значение функции только в одной новой точке, а значит минимизирует необходимое для достижения требуемой точности количество вычислений значений функции \(f(x)\).

Пусть задана требуемая точность delta. Тогда алгоритма поиска минимума функции f на отрезке [a, b] методом золотого сечения состоит из следующих шагов.

1. Найти x1 и x2 по формулам (8).

2. Если f(x1) > f(x2), то a = x1. Иначе, b = x_2.

3. Если b - a < delta, то требуемая точность достигнута и принимается, что c = (a + b) / 2 — положение глобального минимума и работа алгоритма завершается. Иначе, вернуться к шагу №1.

Note

Выбор \(x_1\) и \(x_2\) по формулам (8) позволяет сэкономить вычисления на втором и следующих итерация. Например, если на предыдущей итерации алгоритм попал в ветку, где \(f(x_1) > f(x_2)\), то на следующей итерации \(a = x_1\) и можно показать, что \(x_1\) на следующей итерации совпадает с \(x_2\) на предыдущей и можно переиспользовать вычисленные на предыдущей итерации значения \(x_2\) и \(f(x_2)\) как значения \(x_1\) и \(f(x_1)\) на следующей.

Метод градиентного спуска

Метод градиентного спуска — один из самых распространенных методов минимизации функции. Для его работы требуется не только непрерывность самой функции \(f\), но ещё и непрерывность её первой производной \(f'\).

Известно, что в случае функции нескольких переменных \(f\colon \mathbb{R}^n \to \mathbb{R}\), градиент \(\nabla f(x)\) определяет направление наискорейшего роста в окрестности точки \(x\). И наоборот, в противоположном направлении функция \(f\) убывает быстрее всего. Метод градиентного спуска опирается на это свойство градиента: на каждой итерации алгоритма совершается шаг в направлении антиградиента (\(-\nabla f(x)\)), т.е. направлении наискорейшего спуска.

Градиент \(\nabla f\) функции \(f\colon \mathbb{R} \to \mathbb{R}\) совпадает с её производной и один шаг градиентного спуска в таком случае задается формулой

\[ x_{i + 1} = x_i - \alpha_i f'(x_i), \]

где \(x_i\) — текущее приближение, \(x_{i+1}\) — следующее приближение, а \(\alpha_i\) — шаг градиентного спуска на \(i\)-й итерации.

Если \(f\) строго выпукла, то при наложении определенных требований на последовательность \(\{\alpha_0, \alpha_1, ..., \alpha_i, ...\}\) можно доказать, что метод градиентного спуска сойдется к глобальному минимуму. Но даже при не выполнении этих условий метод градиентного спуска может сойтись, но тогда гарантировать сходимость не представляется возможным. В качестве контроля сходимости иногда используется величина градиента, так как в экстремальной точке дифференцируемой функции производная равна нулю. Иными словами, критерием остановки алгоритма градиентного спуска иногда выступает условие

\[ |f'(x_i + 1)| < \varepsilon. \]

Так как гарантировать достижение даже локального минимума в общем случае невозможно, то также требуется ограничивать максимальное количество итераций, чтобы исключить возможность попадания в бесконечный цикл.

Вам предлагается реализовать метод градиентного спуска с постоянным шагом \(\alpha\).

(9)\[x_{i + 1} = x_i - \alpha f'(x_i).\]

Правильный подбор этого параметра критические влияет на сходимость алгоритма. Слишком маленький шаг потребует много итераций для сходимости и почти наверняка застрянет в первом встреченном локальном минимуме. Слишком большой шаг может разойтись, а может сравнительно быстро сойтись при удачном стечении обстоятельств и почти наверняка проскочит минимум, что хорошо, если минимум локальный, и плохо, если минимум глобальный.

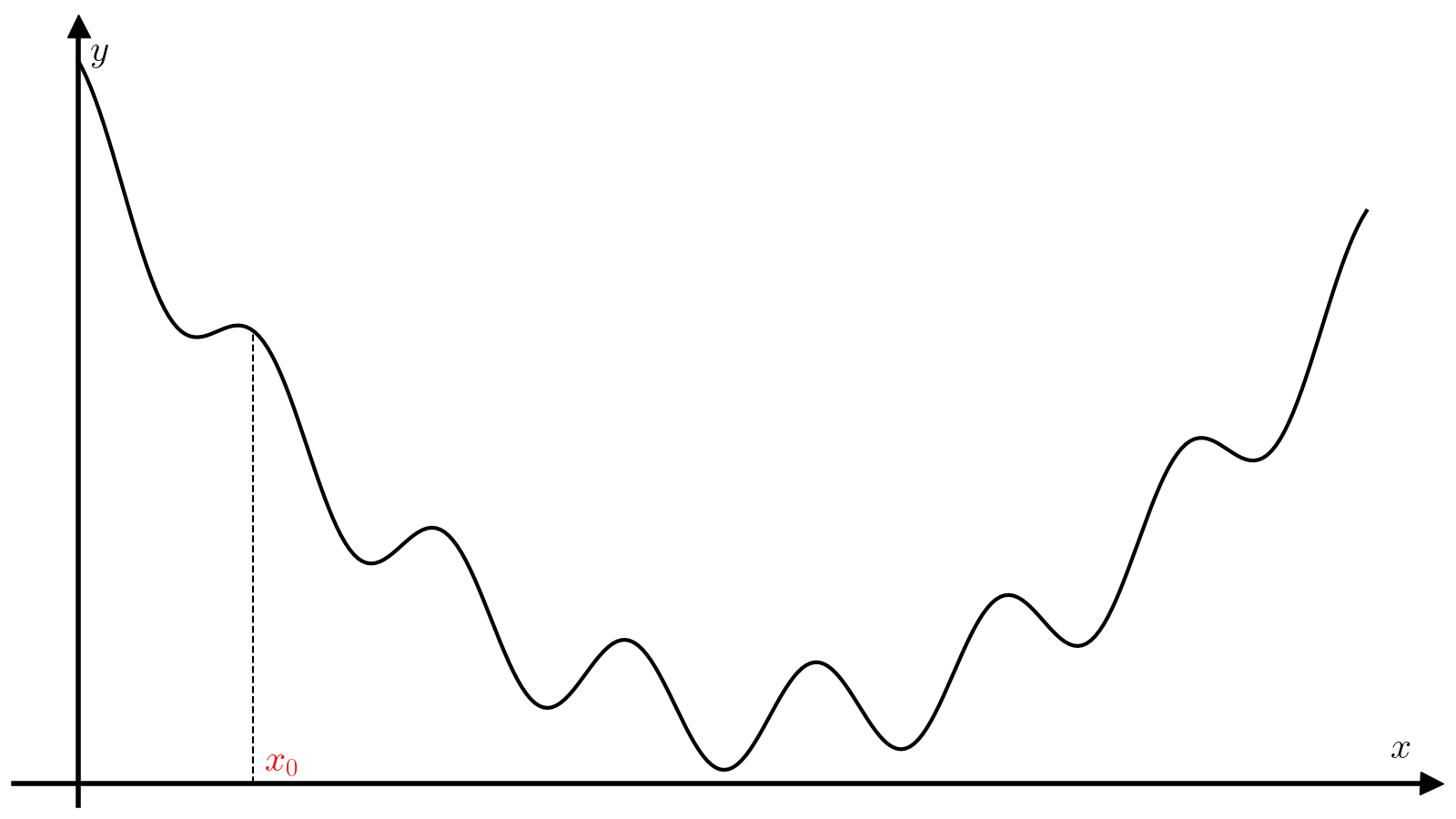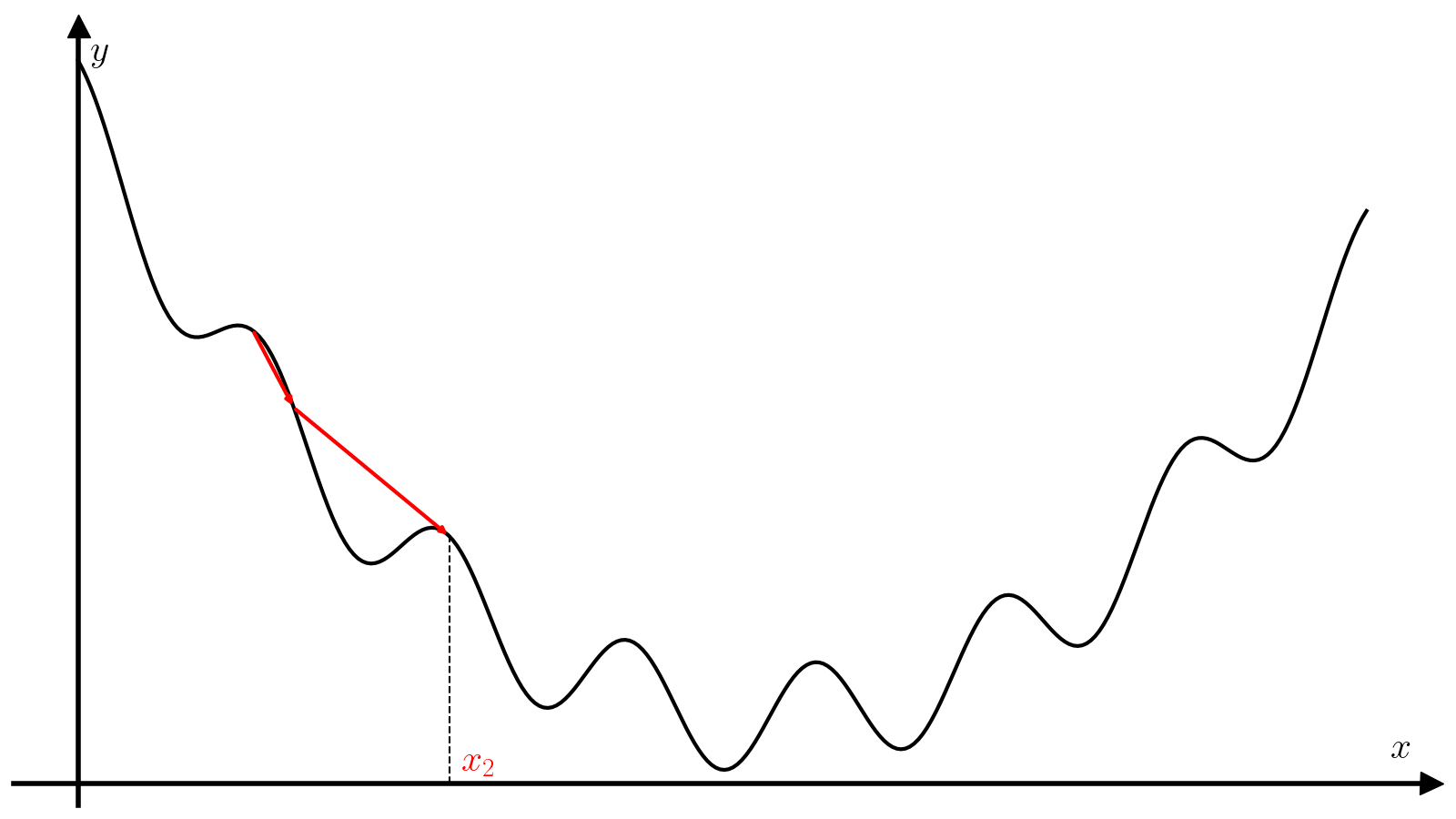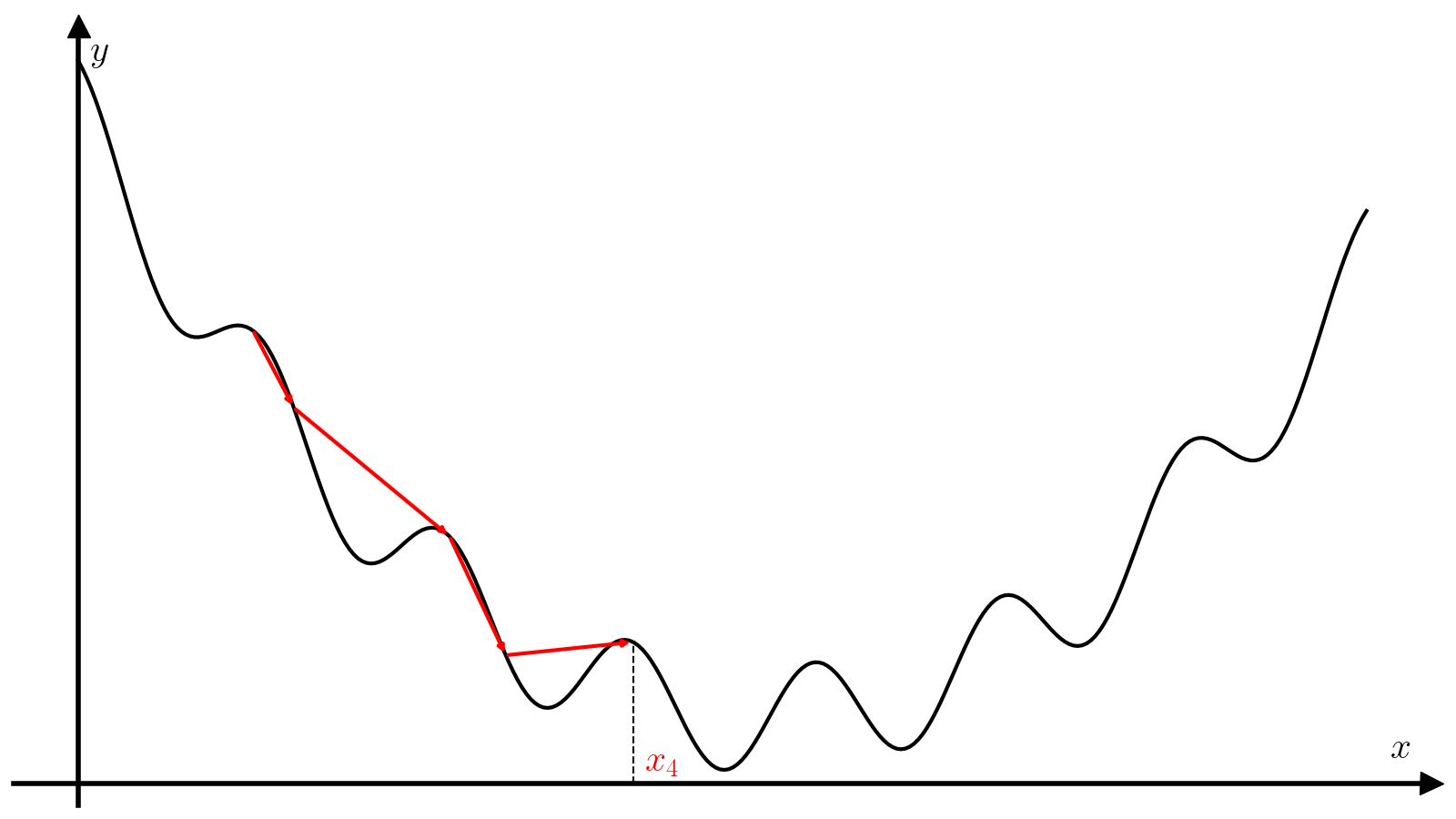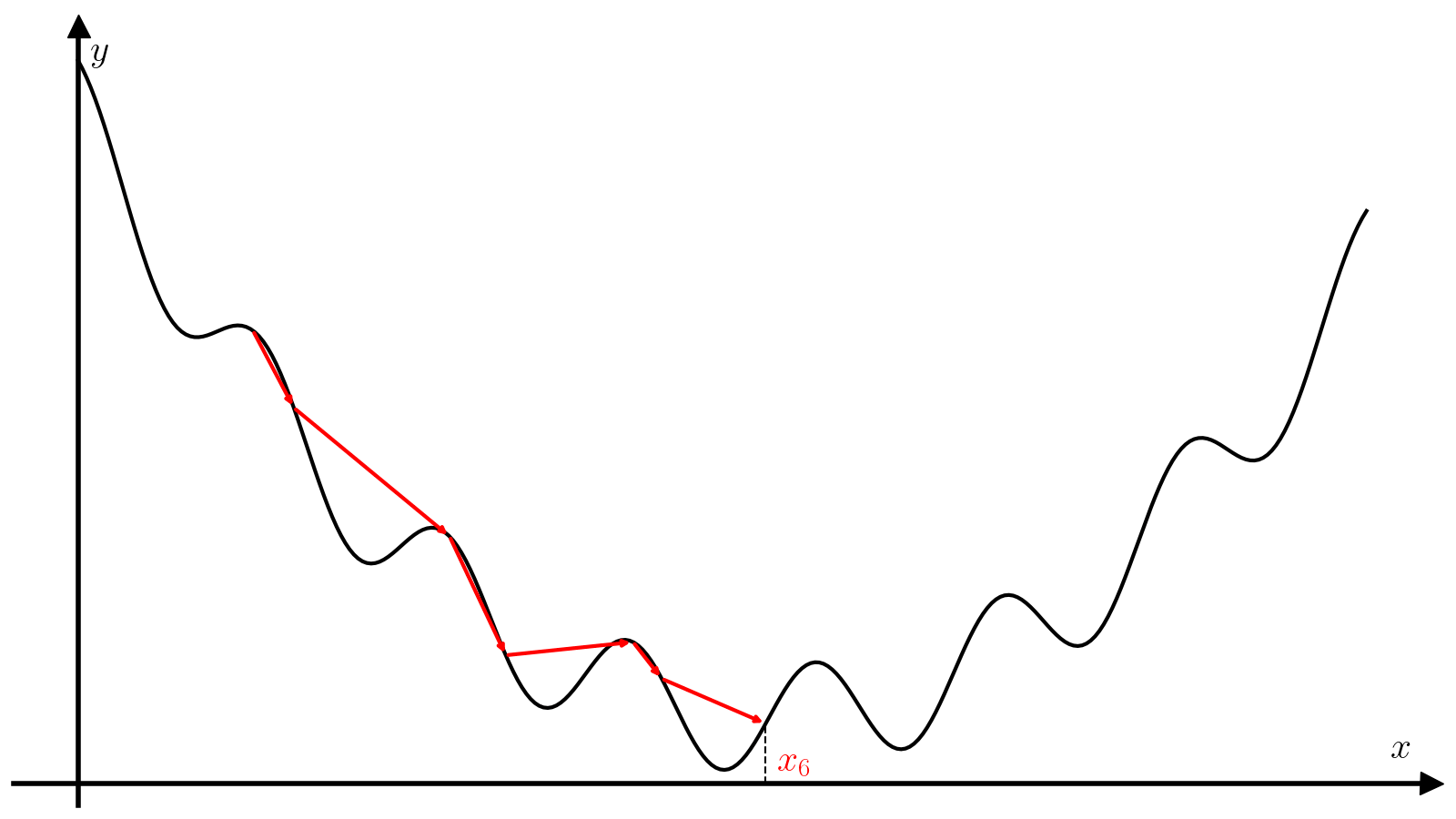
Пусть задана величина epsilon, максимальное число итераций max_iter, шаг градиентного спуска alpha и начальное приближение x0. Тогда алгоритм поиска минимума функции f с производной f_prime на отрезке [a, b] методом золотого сечения состоит из следующих шагов.

1. Инициализировать переменную iter нулем, а переменную x_previous величиной x_next;

2. Найти следующее приближение x_next по формуле (9): x_next = x_previous - alpha * f_prime(x_previous);

3. Если |f_prime(x_next)| < epsilon, то принять, что x_next — найденный минимум, алгоритма завершает свою работу. Иначе, перейти к шагу №4.

4. Увеличить значение переменной iter на 1 и, если iter == max_iter, принять, что метод разошелся и алгоритм завершает работу. Иначе, вернуться к шагу №2.