Задача обнаружения#

import os

import numpy as np
from matplotlib import pyplot as plt
import cv2

image_folder = os.path.join("..", "..", "_static", "lecture_specific", "cv")

def show_image(ax, image, title=None, cmap=None):
    """
    Вывести изображение в указанных осях.
    """
    ax.imshow(image, cmap=cmap)
    ax.set_title(title)
    ax.xaxis.set_visible(False)
    ax.yaxis.set_visible(False)

Поставим задачу автоматического обнаружения монет.

path = os.path.join(image_folder, "coins.jpg")
image = cv2.imread(path, cv2.IMREAD_GRAYSCALE)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, image, cmap="gray")

Обнаружение круглых контуров#

Преобразование Хафа позволяет искать на изображении прямые, окружности, эллипсы и некоторые другие параметрические геометрических элементов.

Так, например, метод cv2.HoughCircles позволяет искать окружности, что может пригодиться в нашей задаче, т.к. монеты имеют округлую форму.

circles = cv2.HoughCircles(image, method=cv2.HOUGH_GRADIENT, dp=2.5, minDist=30, minRadius=10, maxRadius=40)
circles = circles.astype(int).reshape(-1, 3)

green_color = (0, 255, 0)
linewidth = 2
detected_circles = cv2.cvtColor(image, cv2.COLOR_GRAY2RGB)
for (x, y, r) in circles:
    cv2.circle(detected_circles, (int(x), int(y)), int(r), green_color, linewidth)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, detected_circles, cmap="gray")

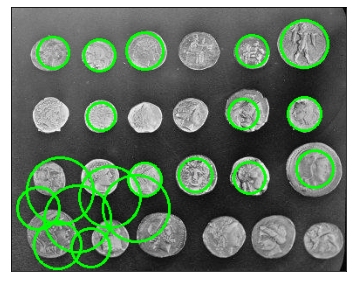
Предварительной обработкой изображения и настройкой параметров метода можно значительно повлиять на качество распознавания окружностей.

blured = cv2.GaussianBlur(image, (9, 9), 0)
blured_canny = cv2.Canny(blured, 100, 180)
circles = cv2.HoughCircles(blured_canny, method=cv2.HOUGH_GRADIENT, dp=2.8, minDist=30, minRadius=10, maxRadius=40)
circles = circles.astype(int).reshape(-1, 3)

green_color = (0, 255, 0)
linewidth = 4
detected_circles = cv2.cvtColor(image, cv2.COLOR_GRAY2RGB)
for (x, y, r) in circles:
    cv2.circle(detected_circles, (int(x), int(y)), int(r), green_color, linewidth)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, detected_circles, cmap="gray")

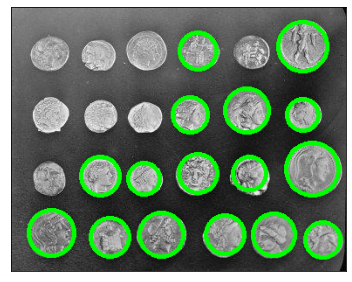
Взаимнокорреляционная функция#

Взаимнокорреляционная функция часто используется для поиска в длинной последовательности более короткой заранее известной. Идея поиска следующая:

наложим короткую последовательность на произвольную позицию в длинной последовательности и посчитаем корреляцию короткой последовательности с той частью длинной, которая попала под короткую;
если эта корреляция достаточно велика, то мы обнаружили короткую последовательность в длинной в этом месте;
повторить шаги 1. и 2. для всех возможных положений короткой последовательности внутри длинной

Посчитаем корреляцию всего изображения с изображением одной монеты.

path = os.path.join(image_folder, "coin.jpg")
pattern = cv2.imread(path, cv2.IMREAD_GRAYSCALE)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, pattern, cmap="gray")

Для этого стандартизируем эти массивы данных и используем функцию scipy.signal.correlate2d, которая позволяет вычислить взаимнокорреляционную функцию двух двухмерных массивов.

from scipy.signal import correlate2d
normalized_image = (image - image.mean()) / image.std()
normalized_pattern = (pattern - pattern.mean()) / pattern.std() 

correlation = correlate2d(normalized_image, normalized_pattern, mode="valid")

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, correlation, cmap="gray")

Получили новое изображение. Его максимумы соответствуют максимальной корреляции изображения монеты с куском исходного изображения.

Нарисуем прямоугольник размера монеты на месте самого большого значения.

x, y = np.unravel_index(correlation.argmax(), correlation.shape)
h, w = pattern.shape

linewidth = 1
detected_coin = cv2.cvtColor(image, cv2.COLOR_GRAY2RGB)
cv2.rectangle(detected_coin, (y, x), (y+w, x+h), green_color, linewidth)


fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, detected_coin, cmap="gray")

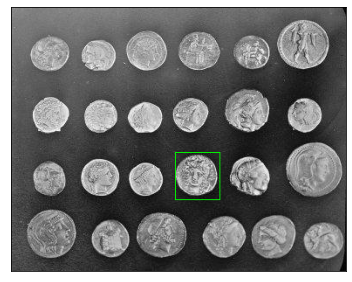
Возьмем 100 наибольших значения и нарисуем на их местах прямоугольники тоже.

indexes = (-correlation).argsort(axis=None)[:100]

detected_coin = cv2.cvtColor(image, cv2.COLOR_GRAY2RGB)
for index in indexes:
    x, y = np.unravel_index(index, correlation.shape)
    cv2.rectangle(detected_coin, (y, x), (y+w, x+h), green_color, linewidth)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, detected_coin, cmap="gray")

Многие прямоугольники оказались почти друг над другом, т.к. в рассматриваемой задаче небольшой сдвиг шаблона вносит малые изменения в коэффициент корреляции.

Чтобы решить эту проблему, отфильтруем все прямоугольники, которые располагаются друг к другу очень близко. Для этого в примере ниже реализована функция фильтрации прямоугольников supression, которая работает по следующему принципу:

Задаём пустой список accepted принятых алгоритмом прямоугольников;
Рассматриваем следующего кандидата в список принятых прямоугольников:
1. Если accepted пуст, то добавляем этого кандидата в список;
2. Иначе добавляем кандидата в список, только если он располагается на превышающем min_dist расстоянии от всех уже принятых прямоугольников из списка accepted.
Повторяем шаг 2 до тех пор, пока не наберется достаточное количество прямоугольников или кандидаты не исчерпаются.

indexes = (-correlation).argsort(axis=None)


def compute_minimum_distance(point, points):
    if not points:
        return np.inf
    
    point, points = np.array([point]), np.array(points)
    diff = point - points
    distances = np.sqrt(np.sum(diff * diff, axis=1))
    return distances.min()


def supression(points, k, min_dist=30):
    accepted_points = []
    for point in points:
        d = compute_minimum_distance(point, accepted_points)
        if d > min_dist:
            accepted_points.append(point)
            if len(accepted_points) == k:
                return accepted_points
            
    return accepted_points


detected_coin = cv2.cvtColor(image, cv2.COLOR_GRAY2RGB)
points = [np.unravel_index(index, correlation.shape) for index in indexes]
to_draw = supression(points, k=24)

for x, y in to_draw:
    cv2.rectangle(detected_coin, (y, x), (y+w, x+h), green_color, linewidth)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, detected_coin, cmap="gray")

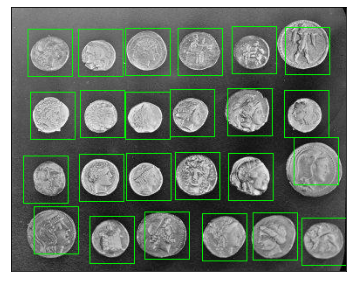
Извлечение признаков#

Воспользуемся специальным методом SIFT, который позволяет находить на изображении такие признаки, которые можно относительно надежно находить на других изображениях того же объекта. Более конкретно этот метод находит на изображении ключевые точки и их дескрипторы (описания), которые позже можно сопоставить с таковыми на другом изображении и при хорошем совпадении считать, что объект обнаружен.

def SIFT_detection(image, pattern):
    orb = cv2.SIFT_create()
    key_points_1, descriptors_1 = orb.detectAndCompute(image, None)
    key_points_2, descriptors_2 = orb.detectAndCompute(pattern, None)

    FLANN_INDEX_KDTREE = 1
    index_params = {
        "algorithm": FLANN_INDEX_KDTREE,
        "trees": 5
    }
    search_params = {"checks": 50} 
    
    flann = cv2.FlannBasedMatcher(index_params, search_params)
    matches = flann.knnMatch(descriptors_1, descriptors_2, k=2)
    
    matchesMask = [[0,0] for i in range(len(matches))]
    for i,(m, n) in enumerate(matches):
        if m.distance < 0.7 * n.distance:
            matchesMask[i]=[1,0]
    
    draw_params = {
        "matchColor": (0, 255, 0),
        "singlePointColor": (255, 0, 0),
        "matchesMask": matchesMask, 
        "flags":  cv2.DrawMatchesFlags_DEFAULT
    }


    return cv2.drawMatchesKnn(
        image, 
        key_points_1, 
        pattern, 
        key_points_2, 
        matches, 
        None, 
        **draw_params
    )

    

Применим этот метод к нашим монетам.

matches = SIFT_detection(pattern, image)

fig, ax = plt.subplots(figsize=(10, 10), layout="tight")
show_image(ax, matches, cmap="gray")

Этот метод имеет свои преимущества в случае, если искомый объект присутствует в изображении с несколько другим ракурсом.

path = os.path.join(image_folder, "shelf.jpg")
image = cv2.imread(path, cv2.IMREAD_GRAYSCALE)

fig, ax = plt.subplots(figsize=(10, 10), layout="tight")
show_image(ax, image, cmap="gray")

path = os.path.join(image_folder, "book.jpg")
pattern = cv2.imread(path, cv2.IMREAD_GRAYSCALE)

fig, ax = plt.subplots(figsize=(5, 5), layout="tight")
show_image(ax, pattern, cmap="gray")

matches = SIFT_detection(image, pattern)

fig, ax = plt.subplots(figsize=(10, 10), layout="tight")
show_image(ax, matches, cmap="gray")

Практикум по компьютерным технологиям

Задача обнаружения

Contents

Задача обнаружения#

Обнаружение круглых контуров#

Взаимнокорреляционная функция#

Извлечение признаков#