Регрессия#

import os

import numpy as np
import pandas as pd
from matplotlib import pyplot as plt
import seaborn as sns
plt.rcParams.update({"font.size": 16})


def generate_problem(function, a, b, randomize_x=False, noise=None, n=50):               
    x = np.random.uniform(low=a, high=b, size=n) if randomize_x else  np.linspace(a, b, n)
    y = function(x)
    if noise:
        y += np.random.normal(loc=0., scale=noise, size=n)
    return pd.DataFrame({
        "x": x,
        "y": y
    })

def plot_regression_problem(ax, data, regressor=None, test_data=None):
    # dataset column
    if test_data is None:
        data = data.copy()
        data["dataset"] = "train"
    else:
        data = pd.concat([data, test_data], keys=["train", "test"])
        data = data.reset_index(level=0).rename(columns={"level_0": "dataset"})
    
    # scatter
    ax.set_ylim([
        data["y"].min() - 0.1,
        data["y"].max() + 0.1
    ])
    sns.scatterplot(data=data, x="x", y="y", hue="dataset", ax=ax)
    
    # regressor
    if regressor: 
        x_min, x_max = data["x"].min(), data["x"].max()
        x = np.linspace(x_min, x_max, 100)
        y = regressor(x)
        sns.lineplot(x=x, y=y, color="green", ax=ax)

Аппроксимация полиномами#

Рассмотрим задачу аппроксимации неизвестной функции одного аргумента. Пусть имеется набор из \(N\) точек \((x_i, y_i) \in\mathbb{R}, \, i=1,\ldots, N\) и перед нами стоит цель найти функцию \(f\colon \mathbb{R}\to\mathbb{R}\), которая бы хорошо аппроксимировала имеющиеся точки. Для этого можно поставить задачу поиска функции \(f\) из класса \(F\) с наименьшей среднеквадратичной ошибкой

\[ \dfrac1N\sum_{i=1}^N(f(x_i) - y_i)^2 \sim \min\limits_{f\in F}. \]

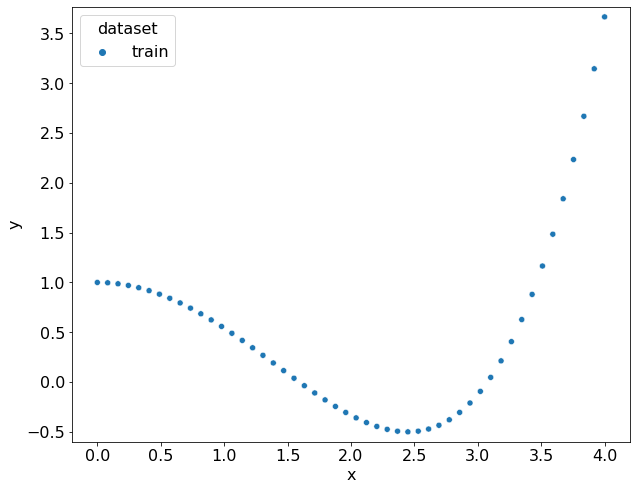
В ячейке ниже генерируется набор таких точек.

значения \(x_i\) генерируются на равномерной сетке на отрезке \([0, 4]\);
значения \(y_i\) генерируются в качестве значения полинома \(y_i = f(x_i) = 1 - \dfrac{x_i^2}{2!} + \dfrac{x_i^4}{4!}\).

from math import factorial
from numpy.polynomial.polynomial import Polynomial

coef = [
    1,                  # 1 
    0,                  # x
    -1./factorial(2),   # x^2
    0,                  # x^3
    1./factorial(4)     # x^4
]
f = Polynomial(coef)

data = generate_problem(f, 0, 4)
fig, ax = plt.subplots(figsize=(10, 8))
plot_regression_problem(ax, data)

data.head()

	x	y	dataset
0	0.00	1.00	train
1	0.08	1.00	train
2	0.16	0.99	train
3	0.24	0.97	train
4	0.33	0.95	train

Если в качестве \(F\) выбрать вообще любые функции, то можно легко найти функцию, которая будет проходить через каждую точку. Ограничимся пока полиномами \(n\)-й степени

\[ P_n(a, x) = a_0 + a_1 x + \ldots + a_n x^n, \]

где \(a=\{a_0, \ldots, a_n\}\) — набор коэффициентов полинома. Тогда задача поиска полинома с наименьшей среднеквадратичной ошибкой сводится в подбору коэффициентов \(a\) методом наименьших квадратов:

\[ \dfrac1N\sum_{i=1}^N(P_n(a, x_i) - y_i)^2 \sim \min\limits_{a\in\mathbb{R}^{n+1}}. \]

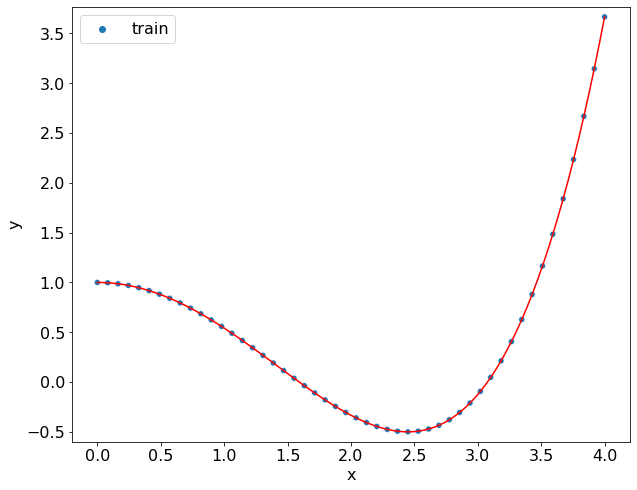
Функция numpy.polyfit позволяет решить именно эту задачу. В ячейке ниже с помощью этого метода удаётся найти хорошую аппроксимацию для этих точек.

def polynomial_regression(data, degree):
    coefficients = np.polyfit(data["x"], data["y"], degree)
    return Polynomial(coef=coefficients[::-1])

polynomial = polynomial_regression(data, 4)

fig, ax = plt.subplots(figsize=(10, 8))
plot_regression_problem(ax, data, polynomial)

for i, (c, c_) in enumerate(zip(coef, polynomial.coef)):
    print(f"x^{i}:\t{c:+.4f} \t {c_:+.4f}")

x^0:	+1.0000 	 +1.0000
x^1:	+0.0000 	 -0.0000
x^2:	-0.5000 	 -0.5000
x^3:	+0.0000 	 -0.0000
x^4:	+0.0417 	 +0.0417

Линейная регрессия#

Пусть \(X\) — матрица Вандермонда для \(x\) координат точек выборки

\[\begin{split} X= \begin{pmatrix} 1 & x_1 & \cdots & x_1^n \\ \vdots & \vdots & \ddots & \vdots \\ 1 & x_N & \cdots & x_N^n \end{pmatrix}, \end{split}\]

\(Y\) — столбец \(y\) координат точек выборки

\[\begin{split} Y = \begin{pmatrix} y_1 \\ \vdots \\ y_n \end{pmatrix}, \end{split}\]

а \(a\) — столбец коэффициентов полинома

\[\begin{split} a = \begin{pmatrix} a_0 \\ a_1 \\ \vdots \\ a_n \end{pmatrix}. \end{split}\]

Тогда матричное уравнение \(X a = Y\) будет соответствовать системе

\[\begin{split} \begin{cases} a_0 + a_1 x_1 + \ldots + a_n x_1^n = y_1, \\ \cdots \\ a_0 + a_1 x_N + \ldots + a_n x_N^n = y_N, \end{cases} \end{split}\]

квадрат невязки которой \(\|X\omega - Y\|^2\) с точностью до множителя равен среднеквадратичной ошибке полинома с коэффициентами \(\{a_0,\ldots, a_n\}\). Эту задачу можно считать линейной регрессией:

регрессия, потому оценивается действительнозначный параметр;
линейная, потому-что параметры модели входят линейно.

В терминах машинного обучения матрица \(X\) — матрица признаков, каждая строка которой соответствует признаковому описанию одной точки, \(Y\) — матрица целевых признаков, а \(a\) — веса модели. Класс sklearn.linear_model.LinearRegression позволяет решать задачу полиномиальной регрессии. Его метод fit принимает на вход матрицу признаков \(X\) и целевых признаков \(Y\) и подбирает коэффициенты методом МНК.

В ячейке ниже переопределяется функция polynomial на основе этого класса. В данном случае приходится явно генерировать матрицу Вандермонда, чтобы задать матрицу признаков.

from sklearn.linear_model import LinearRegression

def polynomial_regression(data, degree):
    X = np.vander(data["x"], N=degree + 1, increasing=True)
    y = data["y"]

    regressor = LinearRegression(fit_intercept=False)
    regressor.fit(X, y)
    return Polynomial(regressor.coef_)

polynomial = polynomial_regression(data, 4)

fig, ax = plt.subplots(figsize=(10, 8))
plot_regression_problem(ax, data, polynomial)

for i, (c, c_) in enumerate(zip(coef, polynomial.coef)):
    print(f"x^{i}:\t{c:+.4f} \t {c_:+.4f}")

x^0:	+1.0000 	 +1.0000
x^1:	+0.0000 	 -0.0000
x^2:	-0.5000 	 -0.5000
x^3:	+0.0000 	 -0.0000
x^4:	+0.0417 	 +0.0417

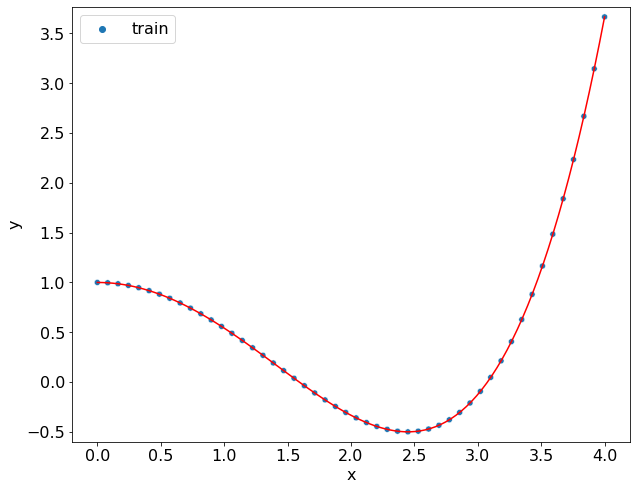
Получили тоже самое решение. Посмотрим влияние степени полинома.

degrees = [0, 1, 2, 3, 4, 5, 6, 20, 40]

coefficients = {}
fig, axs = plt.subplots(figsize=(20, 15), ncols=3, nrows=3, layout="tight")
fig.suptitle("Without noise")
for ax, degree in zip(axs.flatten(), degrees):
    regressor = polynomial_regression(data, degree)
    coefficients[degree] = regressor.coef[:6] 
    plot_regression_problem(ax, data, regressor)
    ax.set_title(f"n={degree}")

coefficients["true"] = coef

with pd.option_context('display.float_format', '{:0.4f}'.format):
    df = pd.DataFrame.from_dict(coefficients, orient="index", columns=[f"x^{i}" for i in range(6)])
    print(df)

        x^0     x^1     x^2     x^3    x^4     x^5
  0.2699     NaN     NaN     NaN    NaN     NaN
  0.2699  0.0000     NaN     NaN    NaN     NaN
  0.5024  0.0000 -0.0268     NaN    NaN     NaN
  0.5024 -0.0000 -0.0268  0.0000    NaN     NaN
  0.6628 -0.0000 -0.0885  0.0000 0.0028     NaN
  0.6628  0.0000 -0.0885 -0.0000 0.0028  0.0000
  0.7721  0.0000 -0.1772  0.0000 0.0130 -0.0000
 0.9870  0.0001 -0.8046 -0.0001 0.4259  0.0000
 0.0000  0.0000 -0.0000  0.0000 0.0000 -0.0000
true 1.0000  0.0000 -0.5000  0.0000 0.0417     NaN

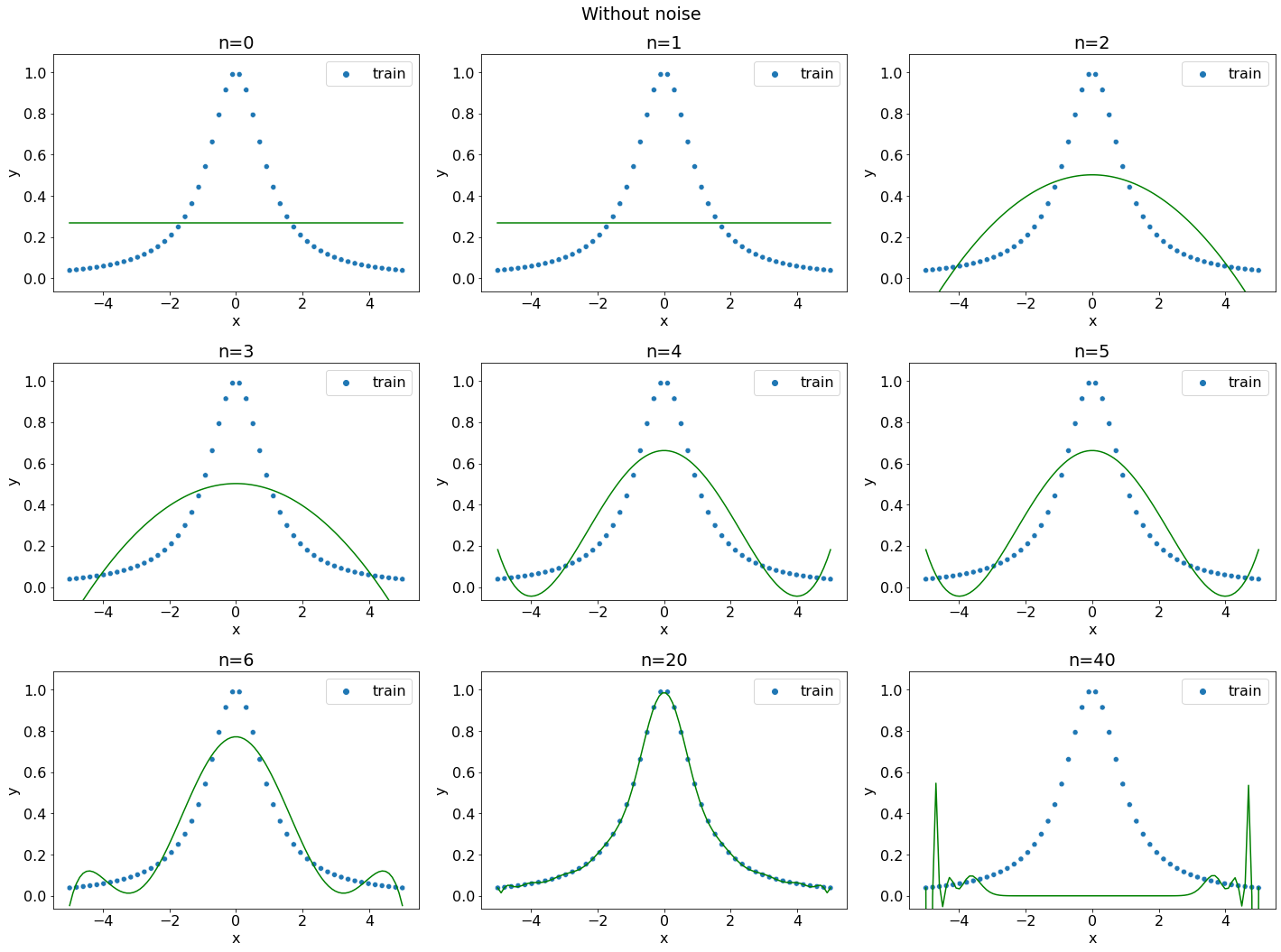
Видим, что

полиномами степеней 0, 1 и 2 совсем не удаётся уловить исходную зависимость \(f(x) = 1 - \dfrac{x^2}{2} + \dfrac{x^4}{12}\);
полином степени 3 в неплохой степени аппроксимирует точки выборки, но коэффициенты найденного полинома довольно сильно отличаются от исходного;
полином степени 4 в точности проходит через все точки выборки. Это объясняется тем, что выборка сгенерирована полиномом 4-й степени, а значит можно точно восстановить все коэффициенты полинома из выборки;
полиномы степеней 5, 6 и 20 находят по факту тот же самый полином четвертой степени с нулевыми коэффициентами при старших степенях, что согласуется с теорией;
при \(N=40\) не удаётся получается аппроксимация плохого качества, что объясняется погрешностью численного алгоритма решения задачи МНК.

Добавим шум к данным и посмотрим, как это повлияет на качество аппроксимации.

data = generate_problem(f, 0, 4, noise=0.2, randomize_x=True)
degrees = [2, 3, 4, 5, 6, 7, 8, 9, 10]


coefficients = {}
fig, axs = plt.subplots(figsize=(20, 15), ncols=3, nrows=3, layout="tight")
fig.suptitle("With noise")
for ax, degree in zip(axs.flatten(), degrees):
    regressor = polynomial_regression(data, degree)
    coefficients[degree] = regressor.coef[:6]
    
    plot_regression_problem(ax, data, regressor)
    ax.set_title(f"n={degree}")
    
coefficients["true"] = coef

with pd.option_context('display.float_format', '{:0.2f}'.format):
    df = pd.DataFrame.from_dict(coefficients, orient="index", columns=[f"x^{i}" for i in range(6)])
    print(df)

       x^0   x^1    x^2    x^3    x^4    x^5
   1.03 -0.52   0.07    NaN    NaN    NaN
   1.23 -1.01   0.35  -0.05    NaN    NaN
   1.08 -0.39  -0.30   0.20  -0.03    NaN
   1.14 -0.77   0.30  -0.18   0.07  -0.01
   1.14 -0.78   0.33  -0.21   0.08  -0.01
   0.49  5.11 -15.64  19.24 -12.16   4.13
  -0.23 12.56 -40.51  58.19 -45.10  20.03
   0.75  1.05   5.69 -31.34  51.46 -41.92
  0.48  4.78 -12.58  12.75  -8.98   8.63
true  1.00  0.00  -0.50   0.00   0.04    NaN

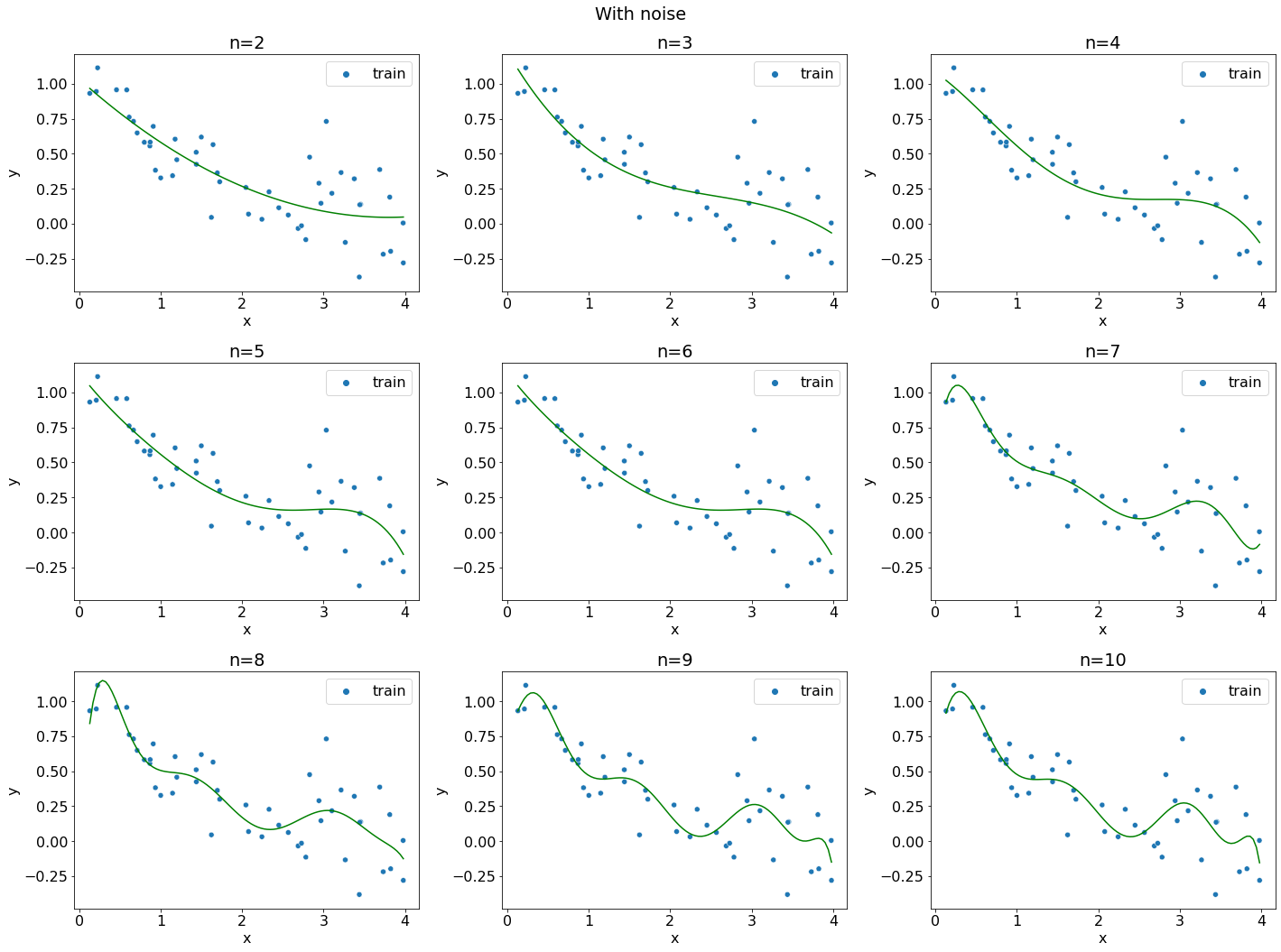
В этот раз коэффициенты исходного полинома не удалось толком восстановить, но все кривые при \(N>3\) довольно неплохо проходят через всю выборку, хотя коэффициенты каждого полинома довольно сильно разнятся. Какой из полиномов выбрать? Какой полином лучше описывает исходную зависимость \(x\) от \(y\)?

До сих пор выборка генерировалась вокруг кривой, которая сама по себе являлась полиномом. Рассмотрим феномен Рунге на другой функции

\[ f(x) = \dfrac{1}{1 + x^2}. \]

def f(x):
    return 1./(1. + x**2)

data = generate_problem(f, -5, 5, n=25)

degrees = (5, 10, 15, 16, 17, 18, 19, 20, 21)

fig, axs = plt.subplots(figsize=(20, 15), ncols=3, nrows=3, layout="tight")
fig.suptitle("With noise")
for ax, degree in zip(axs.flatten(), degrees):
    regressor = polynomial_regression(data, degree)
    
    plot_regression_problem(ax, data, regressor)
    ax.set_title(f"N={degree}")

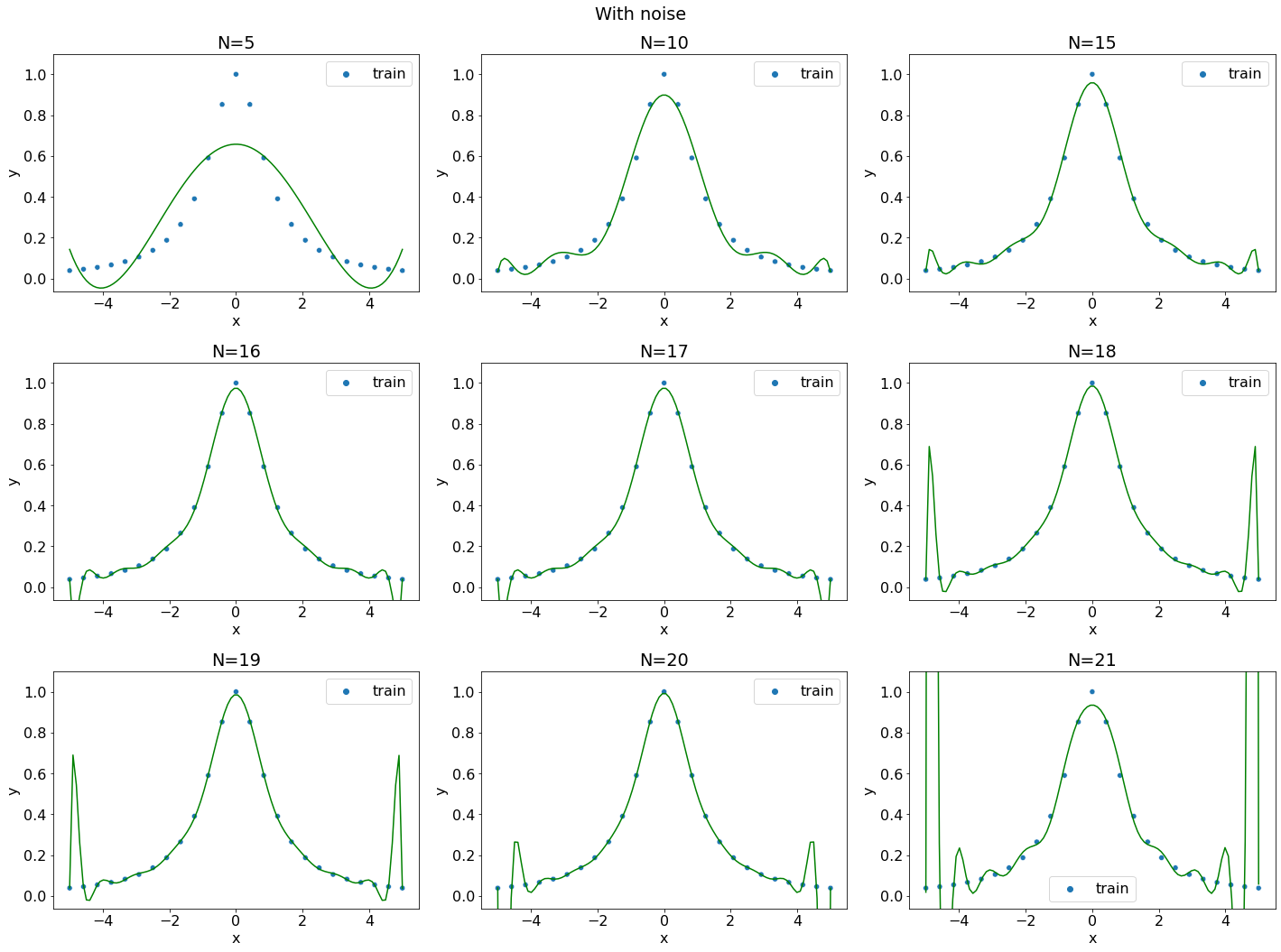
Несмотря на отсутствие шума аппроксимация полиномом высокой степени приводит к нерегулярным решениям на краях. Полином очень близко проходит ко всем точкам выборки, но выдаёт сомнительные значения между ними.

Валидационная выборка. Недообучение и переобучение#

Одна из идей машинного обучения с учителем заключается в следующем: нам не столько интересно насколько хорошо кривая аппроксимирует те точки, под которые мы её подгоняли, а гораздо интереснее обобщающая способность этой кривой, т.е. насколько хорошо эта кривая проходит к тем точкам, которые не никоим образом не использовались для подгонки кривой.

Процесс подбора параметров кривой на основе выборки называют обучением, а саму эту выборку называют обучающей выборкой. Как уже было замечено, нас интересует качество модели на не попавших в обучающую выборку объектах. Т.к. обычно доступная выборка ограниченна, то часто доступную выборку делят на две непересекающиеся части, на одной из которых производят обучение, а на другой тестируют качество модели.

В ячейке эта схема применяется к тому же набору точек. На половине точек подбираются коэффициенты полиномов, но на графике выводятся оба половины выборки.

data = generate_problem(f, -5, 5, n=50)
train_data, test_data = data.iloc[::2], data.iloc[1::2]

fig, axs = plt.subplots(figsize=(20, 15), ncols=3, nrows=3, layout="tight")
fig.suptitle("With noise")
for ax, degree in zip(axs.flatten(), degrees):
    regressor = polynomial_regression(train_data, degree)
    plot_regression_problem(ax, train_data, regressor, test_data)
    ax.set_title(f"n={degree}")

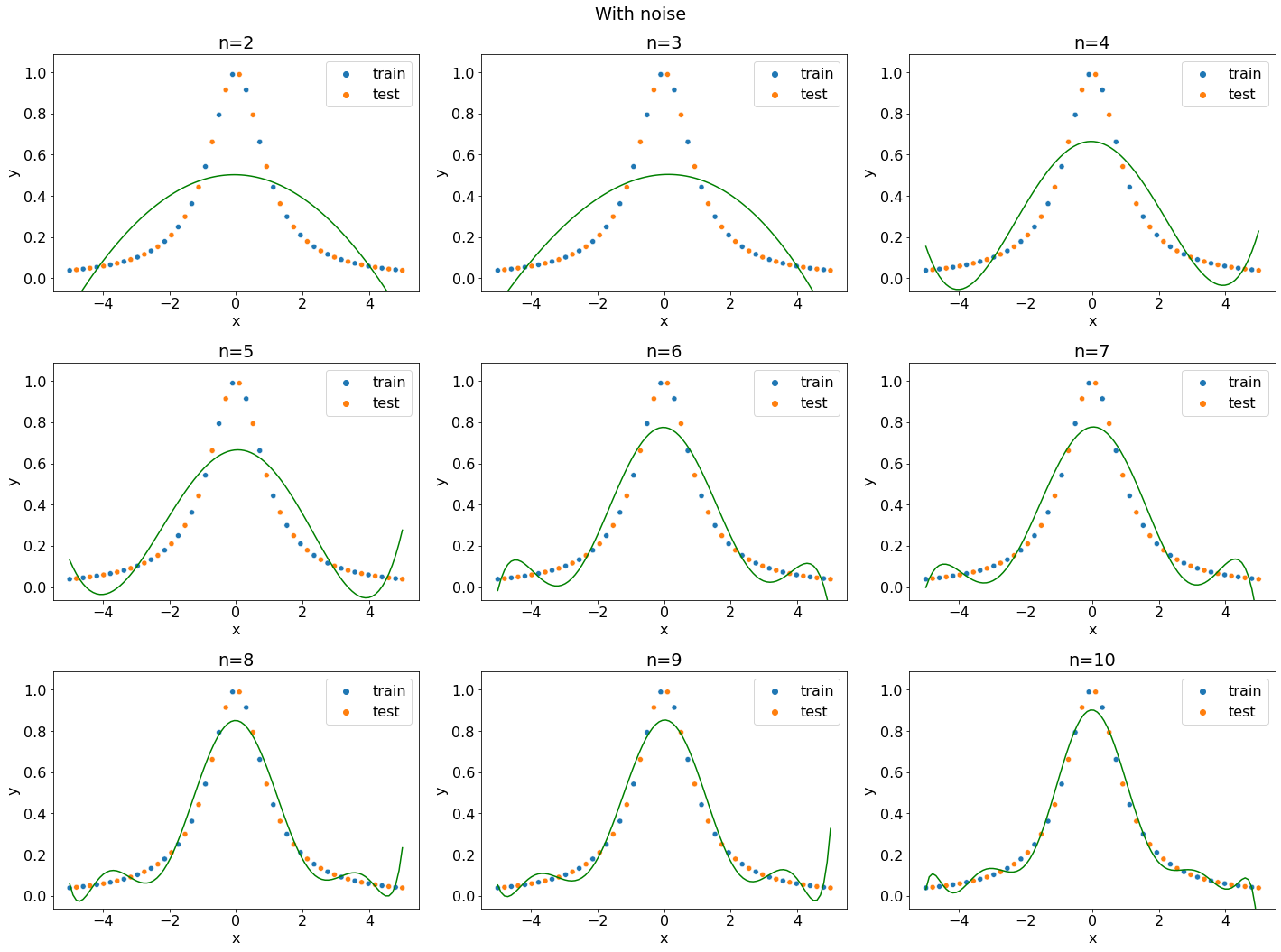
Заметим, что при больших \(N\) кривая проходит близко к точкам обучающей выборки, но далеко от точек валидационной.

fig, ax = plt.subplots(figsize=(10, 7))
regressor = polynomial_regression(train_data, degree=21)
plot_regression_problem(ax, train_data, regressor, test_data)
ax.set_xlim(2, 5)
ax.set_ylim(0, 0.4)

(0.0, 0.4)

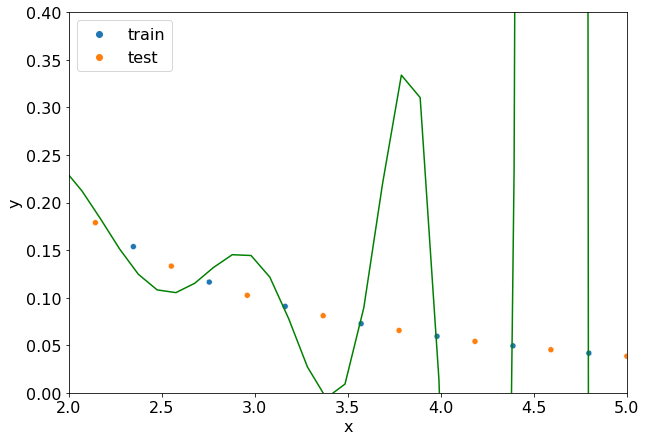
Рассмотрим две крайние ситуации.

Алгоритм плохо аппроксимирует и точки обучающей выборки и точки тестовой выборки. Такой эффект называют недообучением (underfitting) и его можно наблюдать на графиках при малых \(n\). Недообучение часто связывают с слишком простым семейством моделей: полинома 5-й степени просто недостаточно, для того чтобы хоть как-то аппроксимировать кривую \(1./(1 + x^2)\).
Алгоритм хорошо аппроксимирует точки обучающей выборки, но плохо точки тестовой выборки. Такой эффект называют переобучением (overfitting) и его можно наблюдать при больших \(b\). Переобучение часто связывают с слишком сложной моделью: полином высокой степени можно провести через все точки обучающей выборки, т.е. полином может её как-бы запомнить.

В реальных задачах редко можно обучающую выборку. Например, пространство признаков может быть многомерным. В таких ситуациях эффекты обучения/переобучения пытаются обнаружить с помощью подсчета метрик на обучающей и валидационной выборках. Если модель демонстрирует плохие показатели на обеих выборках, то скорее всего алгоритм недообучился, а если алгоритм показывает хорошие показатели на тренировочной выборке, но плохие на валидационной, то скорее всего алгоритм переобучился.

Построим график зависимости среднеквадратичной ошибки в зависимости на обучающей и тестовой выборках в зависимости от степени полинома.

from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error

def evaluate_mse(regressor, data):
    y_pred = regressor(data["x"])
    y_true = data["y"]
    return mean_squared_error(y_true, y_pred)



train_mse = []
test_mse = []
for degree in range(22):
    regressor = polynomial_regression(train_data, degree)
    train_mse.append(evaluate_mse(regressor, train_data))
    test_mse.append(evaluate_mse(regressor, test_data))


fig, ax = plt.subplots(figsize=(15, 7))
ax.plot(train_mse, label="train")
ax.set_yscale("log")
ax.plot(test_mse, label="test")
ax.set_xlabel("n")
ax.set_ylabel("MSE")
ax.legend()

<matplotlib.legend.Legend at 0x18f598f67c0>

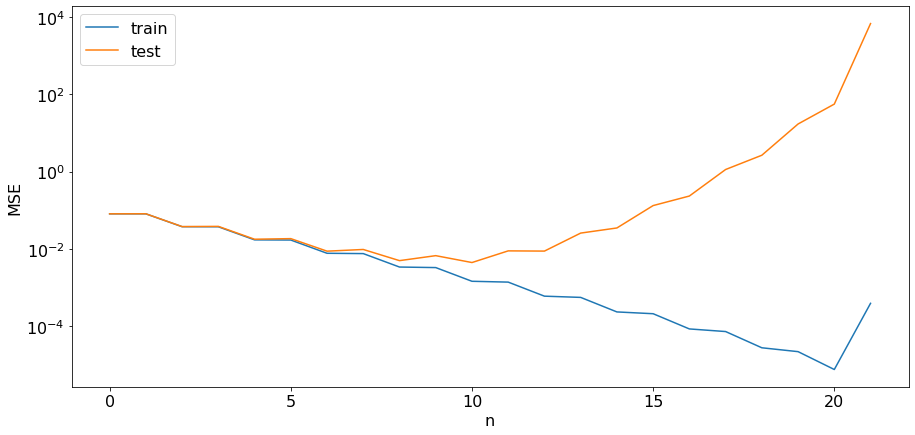
При \(n\) от 1 до примерно 5 погрешность на обучающей и валидационной выборках примерно совпадает, но при увеличении \(N\) погрешность падает. Из этого можно сделать вывод, что алгоритм недообучился. При \(n\) больших 10 погрешность продолжает падать на обучающей выборке, но не на тестовой, что сигнализирует о переобучении. Оптимальное значение \(n\) находится где-то по середине.

Практикум по компьютерным технологиям

Регрессия

Contents

Регрессия#

Аппроксимация полиномами#

Линейная регрессия#

Валидационная выборка. Недообучение и переобучение#