Настройка деталей графиков#

Обычно созданные просто так графики Matplotlib выглядят сыро и необходимо приложить дополнительные усилия, чтобы довести их до ума. Благо Matplotlib позволяет управлять всеми элементами на графике.

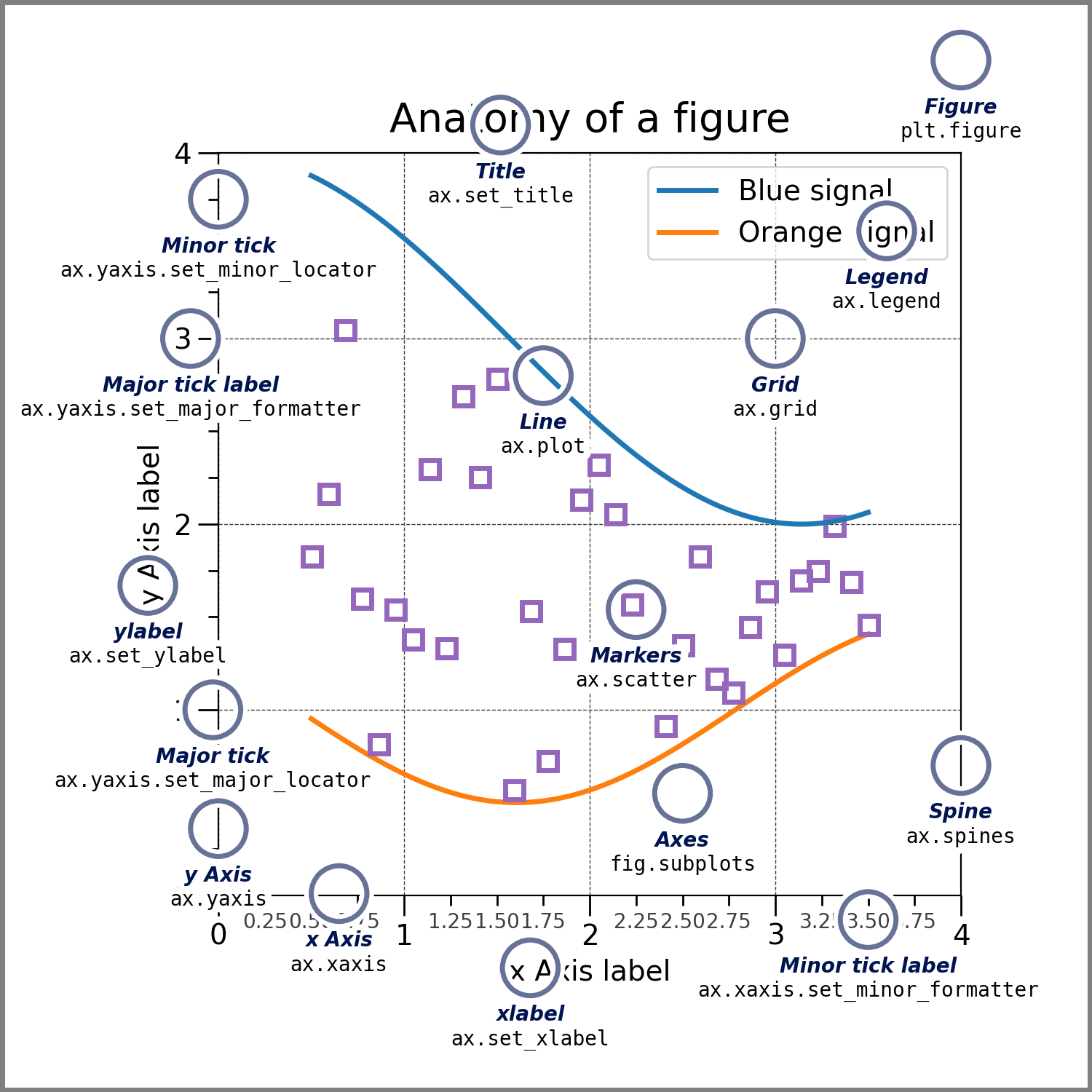
Настройка фигуры#

Фигура несет не так много нагрузки при оформлении графика и большинство самых важных параметров уже было упомянуто.

Размеры фигуры удобнее всего указывать на этапе создания параметром figsize. Он отвечает за размер генерируемого окна с графиком или за размер результирующей картинки при выводе на экран или сохранении в файл.
Заголовок всей фигуры устанавливается методом suptitle;
В качестве макета фигуры (параметр layout) в большинстве ситуаций предпочтительнее использовать значение "tight".

У фигуры ещё можно настроить цвет фона и границ, но в большинстве случаев разумнее воспользоваться готовыми стилями.

import numpy as np
import matplotlib.pyplot as plt

x = np.linspace(0, 2.*np.pi, 100)
y = np.sin(x)


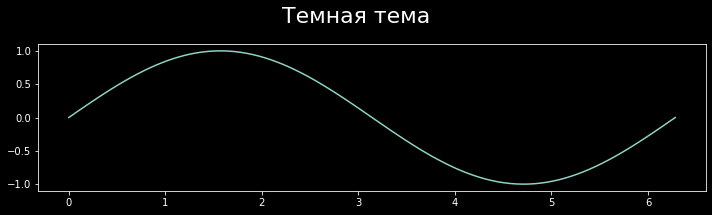
with plt.style.context('dark_background'): # исполнить следующие операции, применяя стиль 'dark_background'
    fig, ax = plt.subplots(figsize=(10, 3), layout="tight")
    fig.suptitle("Темная тема", size=22)
    ax.plot(x, y)

Диапазон значений#

Matplotlib автоматически подбирает диапазон значений, но иногда может потребоваться его изменить, если, например, автоматически подобранный диапазон не охватывает все необходимые элементы на графике или, например, чтобы сфокусировать внимание на какой-то отдельной части графика. В таких случаях всегда можно настроить диапазон вдоль каждой оси методами set_xlim и set_ylim.

Продемонстрируем принцип работы этих методов на примере. Для этого воспользуемся генерирующим снежинку Коха кодом из официальной документации Matplotlib (ссылка). Этот код находится под спойлером ниже.

import numpy as np
import matplotlib.pyplot as plt

def koch_snowflake(order, scale=10):
    """
    Return two lists x, y of point coordinates of the Koch snowflake.

    Parameters
    ----------
    order : int
        The recursion depth.
    scale : float
        The extent of the snowflake (edge length of the base triangle).
    """
    def _koch_snowflake_complex(order):
        if order == 0:
            # initial triangle
            angles = np.array([0, 120, 240]) + 90
            return scale / np.sqrt(3) * np.exp(np.deg2rad(angles) * 1j)
        else:
            ZR = 0.5 - 0.5j * np.sqrt(3) / 3

            p1 = _koch_snowflake_complex(order - 1)  # start points
            p2 = np.roll(p1, shift=-1)  # end points
            dp = p2 - p1  # connection vectors

            new_points = np.empty(len(p1) * 4, dtype=np.complex128)
            new_points[::4] = p1
            new_points[1::4] = p1 + dp / 3
            new_points[2::4] = p1 + dp * ZR
            new_points[3::4] = p1 + dp / 3 * 2
            return new_points

    points = _koch_snowflake_complex(order)
    x, y = points.real, points.imag
    return x, y

Чтобы продемонстрировать фрактальную природу снежинки Коха, построим её целиком, а также отдельный её кусок в разном масштабе. Для этого построим один и тот же график в разных осях, а масштаб внутри каждой пары осей подберем параметрами, отвечающими за диапазон.

import numpy as np
import matplotlib.pyplot as plt
import matplotlib.patches as patches

# генерация данных
x, y = koch_snowflake(order=10)

# создание фигуры с тремя осями и построение одинаковых графиков в них
fig, axs = plt.subplots(figsize=(15, 5), ncols=3, layout="tight")
for ax in axs:
    ax.fill(x, y)

# настройка диапазонов значений по осям и заголовка в первых осях
axs[0].set_xlim(-6, 6)
axs[0].set_ylim(-6, 6)
axs[0].set_title("1:1", size=20)

# настройка диапазонов значений по осям и заголовка во вторых осях
axs[1].set_xlim(-2, 2)
axs[1].set_ylim(2, 6)
axs[1].set_title("3:1", size=20)

# настройка диапазонов значений по осям и заголовка в третьих осях
axs[2].set_xlim(-0.2, 0.2)
axs[2].set_ylim(5.4, 5.8)
axs[2].set_title("30:1", size=20)

Text(0.5, 1.0, '30:1')

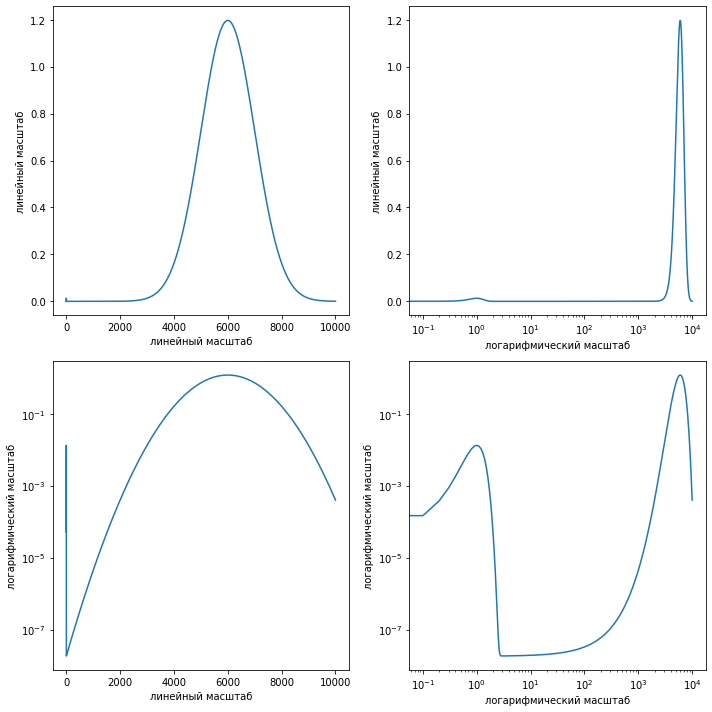
Масштабы осей#

По умолчанию используется линейный масштаб вдоль всех осей, но иногда нагляднее логарифмический масштаб. За масштабы осей отвечают методы set_xscale и set_yscale.

В ячейке ниже демонстрируется применение этих методов.

import numpy as np
from matplotlib import pyplot as plt
from scipy.stats import norm

# генерация данных
x = np.linspace(0, 10000, 100000)
y1 = 0.01 * norm.pdf(x, loc=1, scale=0.3)
y2 = 3000 * norm.pdf(x, loc=6000, scale=1000)
y = y1 + y2

# построение одного и того же графика в четырех осях
fig, axs = plt.subplots(figsize=(10, 10), ncols=2, nrows=2, layout="tight")
for ax in axs.flatten():
    ax.plot(x, y)

# установка масштабов 
axs[0, 0].set_xlabel("линейный масштаб")
axs[0, 0].set_ylabel("линейный масштаб")

axs[0, 1].set_xscale("log")
axs[0, 1].set_xlabel("логарифмический масштаб")
axs[0, 1].set_ylabel("линейный масштаб")

axs[1, 0].set_yscale("log")
axs[1, 0].set_xlabel("линейный масштаб")
axs[1, 0].set_ylabel("логарифмический масштаб")

axs[1, 1].set_xscale("log")
axs[1, 1].set_yscale("log")
axs[1, 1].set_xlabel("логарифмический масштаб")
axs[1, 1].set_ylabel("логарифмический масштаб")

Text(0, 0.5, 'логарифмический масштаб')

Заголовки#

У каждого Axes можно выставить заголовок методом set_title. Полезно помнить, что ещё можно выставить заголовок у всей фигуры целиком.

import numpy as np
from matplotlib import pyplot as plt

fig, (ax1, ax2) = plt.subplots(figsize=(10, 5), ncols=2, layout="tight")
fig.suptitle("Заголовок фигуры", size=22) 

ax1.set_title("Заголовок осей №1", size=20)
ax2.set_title("Заголовок осей №2", size=20)

Text(0.5, 1.0, 'Заголовок осей №2')

Подписи к осям#

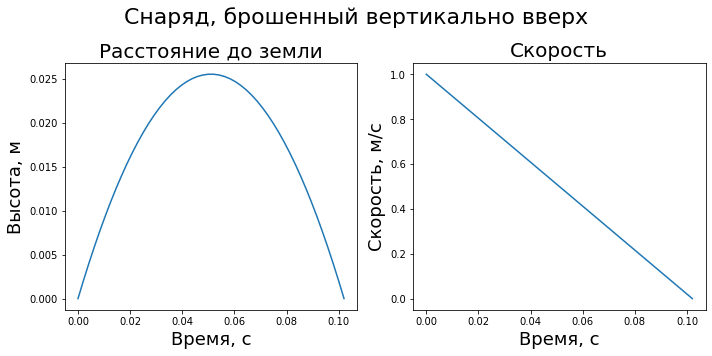
Гораздо проще интерпретировать, что изображено на графике, если в явном виде указано, что отложено по осям. За подписи к осям отвечают методы set_xlabel и set_ylabel.

import numpy as np
from matplotlib import pyplot as plt

# генерация данных
y0 = 0                  # м
v0 = 1                  # м/с
g = 9.8                 # м/(c^2)
t_final = v0 / g

t = np.linspace(0, t_final)   # с
v = v0 - g * t          # м/с
y = y0 + v * t          # м


# создание фигуры с двумя осями
fig, (ax1, ax2) = plt.subplots(figsize=(10, 5), ncols=2, layout="tight")
fig.suptitle("Снаряд, брошенный вертикально вверх", size=22)

# построение графиков в первых осях и подписей к ним
ax1.plot(t, y)
ax1.set_title("Расстояние до земли", size=20)
ax1.set_xlabel("Время, с", size=18)
ax1.set_ylabel("Высота, м", size=18)

# построение графиков во вторых осях и подписей к ним
ax2.plot(t, v)
ax2.set_title("Скорость", size=20)
ax2.set_xlabel("Время, с", size=18)
ax2.set_ylabel("Скорость, м/с", size=18)

Text(0, 0.5, 'Скорость, м/с')

Легенда графика#

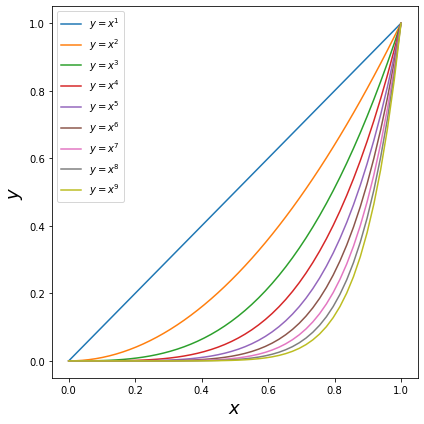
Если в одних осях построено много графиков, то необходимо выводить легенду графика, чтобы можно было визуально определить, какая линия на графике соответствует какой зависимости. Проще всего добиться полноценной легенды следующим образом:

при создании каждого artist указывать label;
в конце вызвать метод legend у осей, чтобы автоматически сформировать легенду графика из указанных меток label.

import numpy as np
from matplotlib import pyplot as plt

x = np.linspace(0, 1)

fig, ax = plt.subplots(figsize=(6, 6), layout="tight")
for power in range(1, 10):
    ax.plot(x, x ** power, label=fr"$y=x^{power}$")
    ax.set_xlabel(f"$x$", size=18)
    ax.set_ylabel(f"$y$", size=18)

ax.legend()

<matplotlib.legend.Legend at 0x2c64c83ac10>

Отсечки и координатная сетка#

Matplotlib автоматически генерирует и набор отсечек (ticks) вдоль осей и подписи к ним (tick label). Например, в примере ниже создаётся вытянутая фигура и Matplotlib генерирует три отсечки по вертикальной оси и 6 отсечек по горизонтальной оси. Каждую из них он подписывает соответствующей координатой с одним знаком после запятой.

fig, ax = plt.subplots(figsize=(10, 1))

При необходимости можно в ручную задавать и набор отсечек и подписи к ним.

Для изменения количества и локацию отсечек удобно использовать методы set_xticks и set_yticks;
Для изменения подписей рядом с ними — методы set_xticklabels и set_yticklabels.

fig, ax = plt.subplots(figsize=(10, 1))
ax.set_xticks([0, 0.5, 1])
ax.set_yticks([0, 0.5, 1])
ax.set_xticklabels(["0", "1/2", "1"])
ax.set_yticklabels(["0", "1/2", "1"])

[Text(0, 0.0, '0'), Text(0, 0.5, '1/2'), Text(0, 1.0, '1')]

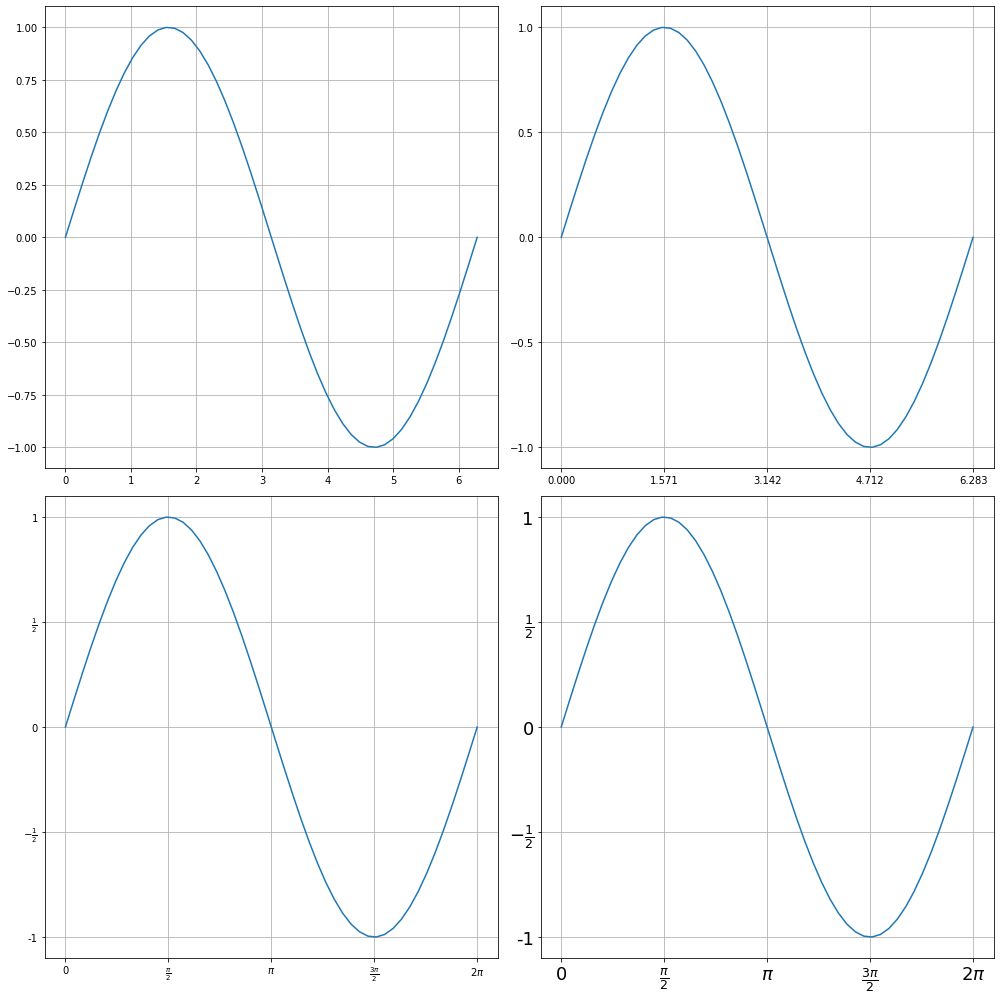
Метод grid включает (или выключает) отображение координатной сетки, линии которой, определяются отсечками вдоль осей.

Ниже демонстрируется применение этих методов.

import numpy as np
from matplotlib import pyplot as plt

# генерация данных
x = np.linspace(0, 2*np.pi)
y = np.sin(x)

# положения отсечек
x_ticks = np.linspace(0, 2*np.pi, 5)
y_ticks = np.linspace(-1, 1, 5)

# метки отсечек
x_tickslabels = ["0", r"$\frac{\pi}{2}$", r"$\pi$", r"$\frac{3\pi}{2}$", r"$2\pi$"]
y_tickslabels = ["-1", r"$-\frac{1}{2}$", "0", r"$\frac{1}{2}$", "1"]
size = 18

# построение одинакового графика в четырех осях
fig, axs = plt.subplots(figsize=(14, 14), ncols=2, nrows=2, layout="tight")
for ax in axs.flatten():
    ax.plot(x, y)
    ax.grid()
    

# изменение только положения отсечек в правых верхних осях
axs[0, 1].set_xticks(x_ticks)
axs[0, 1].set_yticks(y_ticks)

# изменение положение отсечек и их меток в левых нижних осях
axs[1, 0].set_xticks(x_ticks)
axs[1, 0].set_yticks(y_ticks)
axs[1, 0].set_xticklabels(x_tickslabels)
axs[1, 0].set_yticklabels(y_tickslabels)

# указан размер отсечек
axs[1, 1].set_xticks(x_ticks)
axs[1, 1].set_yticks(y_ticks)
axs[1, 1].set_xticklabels(x_tickslabels, size=size)
axs[1, 1].set_yticklabels(y_tickslabels, size=size)

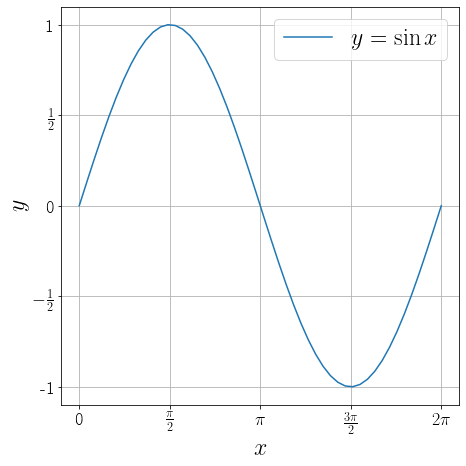
Формулы \(\LaTeX\) в `Matplotlib`#

\(\LaTeX\) изучается только в весеннем семестре курса, но начинать писать формулы на нём можно уже сейчас. Matplotlib умеет вызывать \(\LaTeX\) для рендеринга формул и выводит результат на фигуре, т.е. чтобы это работало, на компьютере должен быть установлен дистрибутив \(\LaTeX\).

Кроме того необходимо явно сказать, чтобы Matplotlib использовал \(\LaTeX\), например следующей командой.

plt.rc('text', usetex=True)

Т.к. \(\LaTeX\) сам по себе не дружит с кириллицей, то может потребоваться подключение пакета babel в преамбуле документа. Сделать это проще всего следующей командой.

plt.rcParams['text.latex.preamble'] = r"""
\usepackage[utf8]{inputenc}
\usepackage[english,russian]{babel}
\usepackage{amsmath}
"""

Ниже воспроизводится последний график из примера выше с использованием \(\LaTeX\) и ещё парой доработок. Подписи на этом графике выглядят гораздо лучше.

import numpy as np
from matplotlib import pyplot as plt
plt.rc('text', usetex=True)
plt.rcParams['text.latex.preamble'] = r"""
\usepackage[utf8]{inputenc}
\usepackage[english,russian]{babel}
\usepackage{amsmath}
"""


# генерация данных
x = np.linspace(0, 2*np.pi)
y = np.sin(x)

# положения отсечек
x_ticks = np.linspace(0, 2*np.pi, 5)
y_ticks = np.linspace(-1, 1, 5)

# метки отсечек
x_tickslabels = ["0", r"$\frac{\pi}{2}$", r"$\pi$", r"$\frac{3\pi}{2}$", r"$2\pi$"]
y_tickslabels = ["-1", r"$-\frac{1}{2}$", "0", r"$\frac{1}{2}$", "1"]
size = 18

fig, ax = plt.subplots(figsize=(7, 7), layout="tight")
ax.plot(x, y, label=r"$y=\sin x$")
ax.legend()

ax.set_xlabel("$x$")
ax.set_ylabel("$y$")

ax.set_xticks(x_ticks)
ax.set_yticks(y_ticks)
ax.set_xticklabels(x_tickslabels, size=size)
ax.set_yticklabels(y_tickslabels, size=size)
ax.grid()

Практикум по компьютерным технологиям

Настройка деталей графиков

Contents

Настройка деталей графиков#

Настройка фигуры#

Диапазон значений#

Масштабы осей#

Заголовки#

Подписи к осям#

Легенда графика#

Отсечки и координатная сетка#

Формулы \(\LaTeX\) в `Matplotlib`#

Практикум по компьютерным технологиям

Настройка деталей графиков

Contents

Настройка деталей графиков#

Настройка фигуры#

Диапазон значений#

Масштабы осей#

Заголовки#

Подписи к осям#

Легенда графика#

Отсечки и координатная сетка#

Формулы \(\LaTeX\) в Matplotlib#

Формулы \(\LaTeX\) в `Matplotlib`#