Дифференцирование и интегрирование функций
Contents
Дифференцирование и интегрирование функций#
from matplotlib import pyplot as plt
def configure_matplotlib():
plt.rc('text', usetex=True)
plt.rcParams["axes.titlesize"] = 28
plt.rcParams["axes.labelsize"] = 24
plt.rcParams["legend.fontsize"] = 24
plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18
plt.rcParams["text.latex.preamble"] = r"""
\usepackage[utf8]{inputenc}
\usepackage[english,russian]{babel}
\usepackage{amsmath}
"""
configure_matplotlib()
Дифференцирование функций#
Разностная производная#
Одно из возможных определений первой производной дифференцируемой функции \(f(x)\) имеет вид
В рамказ компьютерной арифметики предельный переход осуществить невозможно, поэтому в целях аппроксимации производной нередко вместо предела при \(h \to 0\) подставляют очень малое \(h\):
Такая аппроксимация производной называется правой разностной производной. Можно показать, что асимптотическая погрешность вычисления производной таким способом имеет вид \(o(h)\), т.е. уменьшая шаг \(h\) можно добиться любой точности вычисления производной. Более распространенна центральная разнастная производная, определяемая выражением
Её асимптотическая погрешность имеет вид \(o(h^2)\), а значит уменьшая шаг \(h\) в 2 раза, можно ожидать уменьшение погрешности вычисления производной в 4 раза.
Аналогичным образом можно определить аппроксимацию производной любого порядка. Метод scipy.misc.derivative в SciPy вычисляет разностную производную произвольного порядка (опциональный параметр n).
Продемонстрируем его применение на примере функции \(f(x) = e^{2x}\).
from scipy.misc import derivative
import numpy as np
def f(x):
return np.exp(2. * x)
fig, ax = plt.subplots(figsize=(6, 6), layout="tight")
x = np.linspace(-1, 0, 100)
labels = ("$f(x)$", "$f'(x)$", "$f''(x)$")
for n, label in enumerate(labels):
y = derivative(f, x, n=n, dx=1e-3, order=2*n+1) if order > 0 else f(x)
ax.plot(x, y, label=label)
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.legend()
ax.grid()
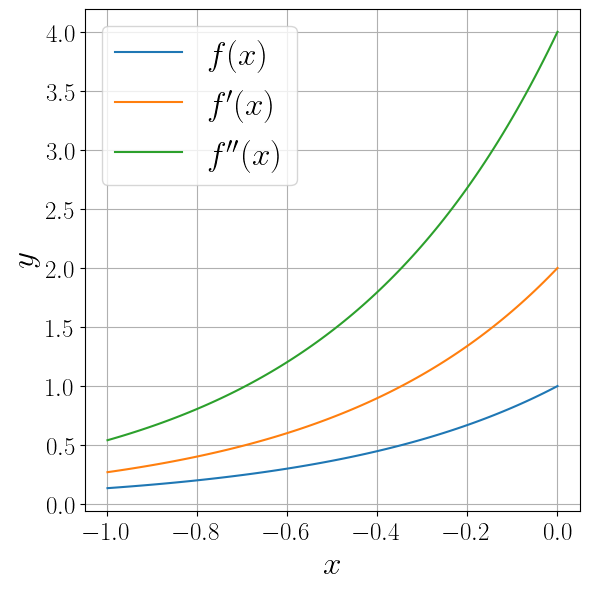
Аналитическое дифференцирование#
Ряд современных библиотек умеет вычислять производные от своих методов. Например, библиотека autograd.
Note
Обратите внимание, что для аналитического вычисления производной средствами библиотеки autograd, необходимо вместо библиотеки NumPy использовать модуль autograd.numpy.
from autograd import numpy as np
from autograd import elementwise_grad
fig, ax = plt.subplots(figsize=(6, 6), layout="tight")
x = np.linspace(-1, 0, 100)
labels = ("$f(x)$", "$f'(x)$", "$f''(x)$")
funcs = (f, elementwise_grad(f), elementwise_grad(elementwise_grad(f)))
for order, (label, func) in enumerate(zip(labels, funcs)):
ax.plot(x, func(x), label=label)
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.legend()
ax.grid()
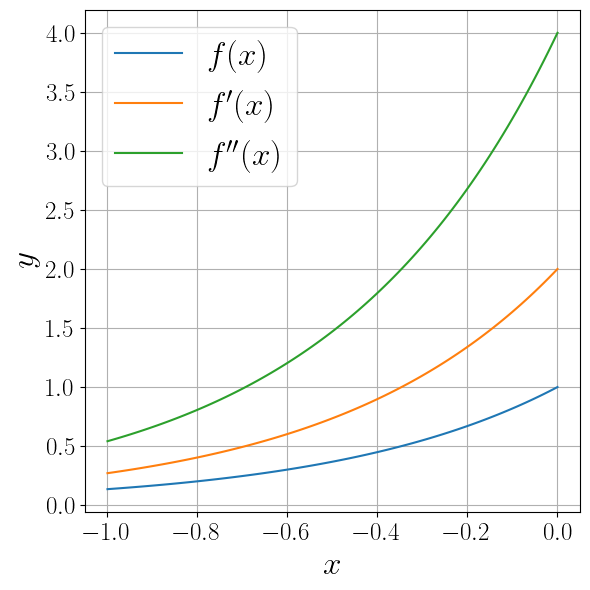
Интегрирование функций#
Подмодуль scipy.integrate позволяет приближенно вычислять значение определенных интегралов.
Однократные интегралы#
Функция scipy.integrate.quad позволяет проинтегрировать функцию \(f\colon \mathbb{R} \to \mathbb{R}\). Вызов функции quad(f, a, b) приближенно находит значение интеграла
В качестве примера найдем численно значение интеграла
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt
f = np.sin
a, b = 0, np.pi
I, _ = integrate.quad(f, 0, np.pi)
x = np.linspace(0, np.pi, 100)
y = f(x)
fig, ax = plt.subplots(figsize=(10, 6), layout="tight")
ax.plot(x, y, label=r"$f(x)=\sin x$")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30)
ax.set_xticks(np.linspace(0, np.pi, 7))
ax.text(np.pi/2, 0.5, fr"$S = {I}$", fontdict={"size": 24, "ha": "center"})
ax.legend()
ax.grid()
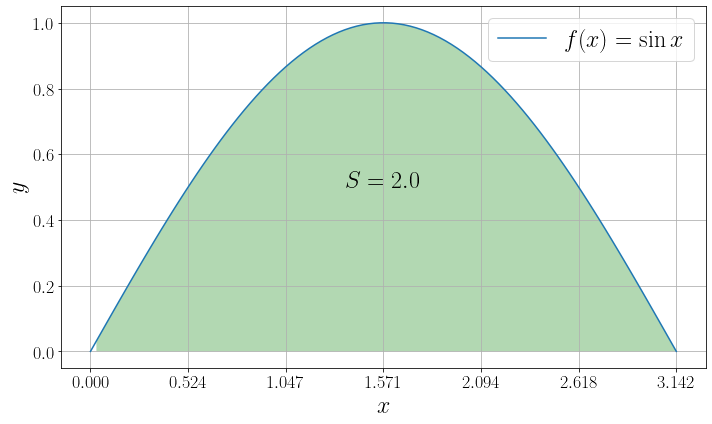
Параметры \(a\) и \(b\) могут принимать значения -inf и +inf, чтобы брать несобственные интегралы. Продемонстрируем это на примере интеграла
def f(x):
return 1. / np.square(x)
a, b = 1, np.inf
I, _ = integrate.quad(f, a, b)
x = np.linspace(a, 7, 100)
y = f(x)
fig, ax = plt.subplots(figsize=(10, 6), layout="tight")
ax.plot(x, y, label=r"$f(x)=\dfrac{1}{x^2}$")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.fill_between(x, np.zeros_like(x), y, where=(y>0), facecolor='green', alpha=0.30)
ax.set_xticks(np.linspace(1, 7, 7))
ax.text(1.5, 0.1, fr"$S = {I}$", fontdict={"size": 24, "ha": "center"})
ax.legend()
ax.grid()
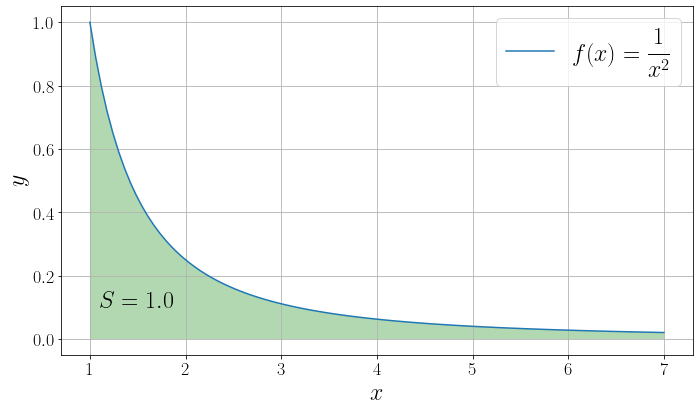
Однако численное взятие несобственных интегралов отнюдь не тривиальная задача. Например, интеграл Френеля $\( \int\limits_0^\infty \sin x^2 \, dx = \sqrt{\dfrac{\pi}{8}} \)$
просто так вычислить не удастся.
def f(t):
return np.sin(t**2)
I, _ = integrate.quad(f, 0, np.inf)
print(I)
-2395.5826175299862
C:\Users\fadeev\AppData\Local\Temp/ipykernel_8252/3166585030.py:4: IntegrationWarning: The integral is probably divergent, or slowly convergent.
I, _ = integrate.quad(f, 0, np.inf)
Интегралы большей кратности#
Функция scipy.integrate.dblquad позволяет вычислять интегралы вида
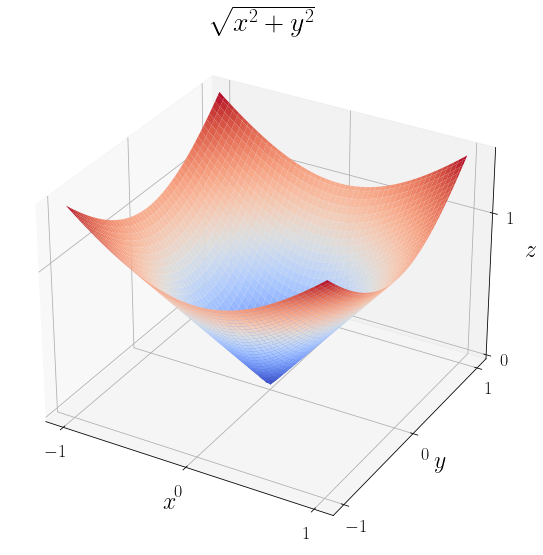
В качестве примера возьмём интеграл функции \(f = \sqrt{x^2 + y^2}\) в области \(D\) совпадающей с кругом единичного радиуса с центром в начале:
import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt
def h(x):
return np.sqrt(1 - x**2)
def g(x):
return -h(x)
def f(x, y):
return np.sqrt(x**2 + y**2)
a, b = -1, 1
I, _ = integrate.dblquad(f, -1, 1, g, h)
x = np.linspace(a, b, 100)
y = np.linspace(a, b, 100)
x, y = np.meshgrid(x, y)
z = f(x, y)
fig, ax = plt.subplots(figsize=(8, 8), layout="tight", subplot_kw={"projection": "3d"})
ax.plot_surface(x, y, z, cmap="coolwarm")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.set_zlabel("$z$")
ax.set_xticks([-1, 0, 1])
ax.set_yticks([-1, 0, 1])
ax.set_zticks([0, 1])
ax.set_title(r"$\sqrt{x^2 + y^2}$")
print(f"Вычисленное значение интеграла: {I}, точное значение: {2*np.pi/3}.")
Вычисленное значение интеграла: 2.0943951023924106, точное значение: 2.0943951023931953.
Трехкратные интегралы вида
можно вычислить методом integrate.tplquad. Интеграл произвольной кратности можно вычислить методом integrate.tplquad.


