NumPy
Contents
NumPy#
horizontal_line = "_" * 80
Первая сторонняя библиотека, с которой мы познакомимся — NumPy (Numerical Python).
Библиотека NumPy предоставляет доступ к многомерным массивам однородных данных (одного типа, обычно числа), подобным массивам C/C++, и к методам их обработки. Под капотом эти самые массивы реализованы с помощью динамических массивов C, которые в отличие от списков хранят непосредственно данные, а не указатели на них.
Зачем нужен NumPy#
Необходимость в специальной библиотеке для работы с большими массивами чисел возникает из-за скорости работы python. За гибкость, выразительность, динамическую типизацию и многие другие достоинства python приходится платить скоростью: код написанный на python, практически всегда будет работать медленнее, чем аналогичный код, написанный на C/C++. Проще всего продемонстрировать это на примере с громоздкими циклами.
#include <iostream>
#include <chrono>
#include <vector>
#include <random>
#define N 10000000
int main(){
// Готовим генератор случайных чисел в промежутке от -1 до 1
std::random_device rd;
std::mt19937 gen(rd());
std::uniform_real_distribution<> dis(-1.0, 1.0);
// Создаём массивы случайных чисел
std::vector<double> a(N), b(N), c(N);
for(int i=0; i < N; ++i){
a[i] = dis(gen);
b[i] = dis(gen);
}
// Измеряем время сложения векторов
auto t1 = std::chrono::high_resolution_clock::now();
for(int i = 0; i < N; ++i)
c[i] = a[i] + b[i];
auto t2 = std::chrono::high_resolution_clock::now();
auto ms_int = std::chrono::duration_cast<std::chrono::milliseconds>(t2 - t1);
std::cout << ms_int.count() << " ms";
}
from time import perf_counter
from random import uniform
N = 10_000_000
# Создаём списки случайных чисел
a = [uniform(-1, 1) for i in range(N)] # новый синтаксис, список случайных чисел
b = [uniform(-1, 1) for i in range(N)]
c = [0.] * N
# Измеряем время сложения этих списков
t1 = perf_counter()
for i in range(N):
c[i] = a[i] + b[i]
t2 = perf_counter()
print(f"{(t2 - t1) * 1000} ms") # perf_counter() - время в секундах
Note
Документацию по модулю time можно найти по этой ссылке, а по модулю random по этой ссылке.
Выше приведено содержимое двух файлов с исходным кодом, каждый из которых складывает два вектора чисел размерности \(10^8\).
Первый файл на языке
C++использует для представления векторов в программе std::vector.Второй файл на языке
pythonиспользует для представления векторов в программе списки.
Эти файлы располагаются по ссылке и могут быть запущены следующими командами в командной строке.
g++ loops.cpp -O2 -o loops
.\loops.exe
python loops.py
В среднем я получил следующие результаты.
|
|
|---|---|
25 ms |
1700 ms |
Note
Вообще говоря, на эти цифры может повлиять огромное количество факторов, в том числе и случайных. Тем не менее разница настолько явная, что качественная картина ясна: циклы в C/C++ работают заметно быстрее, чем в python.
“Среднее” приложение на python не сталкивается с обработкой больших объемов данных и обычно разница в производительности компенсируется затраченным на реализацию алгоритма временем. Но научные вычисления очень часто представляют собой “программы по перемолке чисел” и такое замедление существенно.
Чтобы совместить скорость компилируемого языка и удобство python многие библиотеки поставляются вместе со скомпилированными модулями, написанными на C/C++ (или другом компилируемом языке), а в python “прокидывают” интерфейс для взаимодействия с ними. NumPy — яркий пример такой библиотеки.
Установка NumPy#
В anaconda NumPy установлен по умолчанию, а установить его с помощью PyPI можно следующей командой.
python -m pip install numpy
Установив NumPy, чтобы пользоваться им в программе, необходимо его импортировать.
import numpy as np
Библиотека NumPy используется настолько часто и настолько многими, что сложилась традиция импортировать NumPy с псевдонимом np. Любой программист, увидев где-то в коде выражение вида np.some_method() догадается, что вызывается метод some_method из библиотеки NumPy и ему не потребуется искать глазами определение объекта np, чтобы понять, что скрывается за этим именем.
О массивах NumPy. Тип данных, размерность, оси и форма.#
В ячейке ниже создаётся массив NumPy из случайных чисел. Можете пока не вникать, как конкретно он создаётся. Важно лишь понять, что имя array связывается с каким-то массивом NumPy.
array = np.random.random(size=(2, 3))
print(array)
[[0.5971054 0.44687181 0.63247176]
[0.20003964 0.08926428 0.99762199]]
Массивы в библиотеке представляются типом numpy.ndarray (n dimensional array, n-мерный массив).
print(f"{type(array)=}")
type(array)=<class 'numpy.ndarray'>
Тип ndarray является типизированным контейнером данных, т.е. он предназначен для хранения данных одного и того же типа данных. Тип данных массива хранится в атрибуте dtype (data type). Этих типов может быть много, но большинство из них — стандартные числовые типы C/C++: np.bool8, np.int8, np.int16, np.int32, np.int64, np.unit8, np.unit16, np.unit32, np.uint64, np.float16, np.float32, np.float64, np.complex64, np.complex128 (подробнее про типы данных).
Note
Целые числа в массивах NumPy введут себя совсем не как тип int из python: они всегда занимают определенное количество байт и могут переполняться, т.е. совпадают с целочисленными типами из C/C++.
Note
Вообще говоря, в массивах NumPy можно хранить и объекты произвольного типа, но тогда вместо самих объектов, в массиве будут храниться ссылки на них. Чаще всего массивы NumPy используются все же для хранения чисел.
print(f"{array.dtype=}")
array.dtype=dtype('float64')
Исходя из значения атрибута dtype массива array можно понять, что он хранит в себе 64-битные числа с плавающей запятой.
Ещё NumPy массивы хранят количество своих измерений в атрибуте ndim (number of dimensions). Массивы NumPy могут быть любой размерности: одномерные массивы часто используются для представления векторов, двумерные — для представления матриц и таблиц, массивы более высоких размерностей — для представления тензоров, массивы любых размерностей часто используются для представления значений некоторой функции векторного аргумента на сетке в многомерном пространстве.
print(f"{array.ndim=}")
array.ndim=2
Исходя из значения атрибута ndim массива array видим, что он является двухмерным.
Ещё обязательный атрибут массивов NumPy — форма (shape) — размеры массива вдоль каждого измерения. Эти измерения называются осями (axis в ед. числе и axes в мн. числе).
print(f"{array.shape=}")
array.shape=(2, 3)
Атрибут shape массива array говорит нам, что у него есть 2 элемента вдоль первого измерения и 3 вдоль второго. Иными словами можно сказать, что это таблица из двух строк и трех столбцов.
Общее количество элементов в массиве (произведение количеств элементов вдоль каждой из осей) хранится в атрибуте size.
print(f"{array.size=}")
array.size=6
Все массивы должны быть выравненными, т.е. не может быть матрицы со строками разных длин, трехмерного массива из матриц разных размеров и т.п.
Картинка ниже наглядно иллюстрирует смысл всех только что введенных понятий.
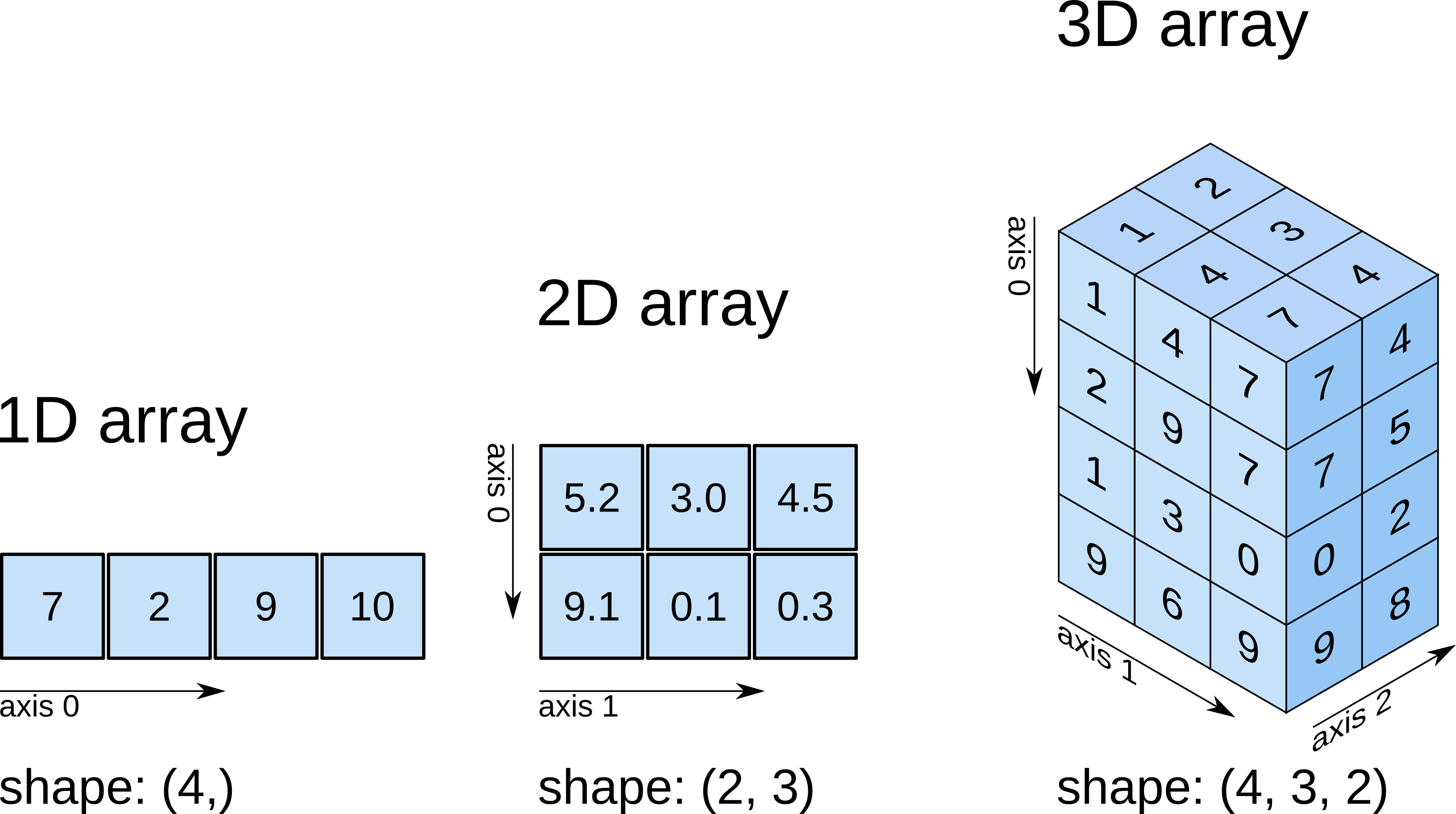
Создание массивов#
Создавать массивы NumPy — ndarray — можно огромным количеством образом, но для их создания редко используется конструктор самого типа. Вместо этого гораздо чаще используются другие методы. Например, метод numpy.array конструирует ndarray из других объектов.
Чаще всего он используется для создания массивов NumPy из python списков чисел. Тип данных выводится как самый общий тип данных, если он не указан явно именованным параметром dtype.
Ниже создаётся одномерный массив из списка четырёх чисел. При этом тип данных явно не указывается и в итоге получается массив чисел с плавающей точкой (float64), т.к. в исходном списке были числа типа int и float.
a1D = np.array([1., 2, 3, 4])
print(repr(a1D))
print(f"{a1D.dtype=}")
print(f"{a1D.ndim=}")
print(f"{a1D.shape=}")
array([1., 2., 3., 4.])
a1D.dtype=dtype('float64')
a1D.ndim=1
a1D.shape=(4,)
В ячейке ниже демонстрируется, как создаются двухмерные массивы. Для этого ей на вход передаются списки списков, где каждый вложенный список — строка будущей таблицы. Т.к. внутри всех этих списков находятся только целые числа, то итоговый тип массива тоже целочисленный.
a2D = np.array([[1, 2], [3, 4]])
print(repr(a2D))
print(f"{a2D.dtype=}")
print(f"{a2D.ndim=}")
print(f"{a2D.shape=}")
array([[1, 2],
[3, 4]])
a2D.dtype=dtype('int32')
a2D.ndim=2
a2D.shape=(2, 2)
Трехмерные массивы создаются по аналогии. В ячейке ниже приводится пример. Обратите внимание, что все числа в передаваемом списке списков списков целочисленного типа, но результирующий массив получается типа float32, т.к. этот тип явно указан при создании массива.
a3D = np.array([[[1, 2], [3, 4]], [[5, 6], [7, 8]]], dtype=np.float32)
print(repr(a3D))
print(f"{a3D.dtype=}")
print(f"{a3D.ndim=}")
print(f"{a3D.shape=}")
array([[[1., 2.],
[3., 4.]],
[[5., 6.],
[7., 8.]]], dtype=float32)
a3D.dtype=dtype('float32')
a3D.ndim=3
a3D.shape=(2, 2, 2)
Так же есть ряд встроенных функций, создающих массивы. Каждая из них принимает в качестве опционального аргумента dtype.
Метод |
Аргументы |
Описание |
|---|---|---|
|
Аналог |
|
|
Разбиение отрезка [ |
|
|
Массив заданной формы из нулей |
|
|
Массив заданной формы из единиц |
|
Не метод, а подмодуль, содержащий методы создания массивов случайных значений |
||
|
Если |
|
|
Матрица с вектором |
|
|
Матрица Вандермонда из вектора |
Продемонстрируем ключевые из них. Массив из нулей создаётся методом np.zeros, который на вход принимает форму массива.
zeros = np.zeros(shape=(2, 2))
print(zeros)
[[0. 0.]
[0. 0.]]
Функция np.ones делает то же самое, но создаёт массив из единиц.
ones = np.ones(shape=(2, 2))
print(ones)
[[1. 1.]
[1. 1.]]
Функция np.eye часто создаётся для создания единичных матриц.
eye = np.eye(2)
print(eye)
[[1. 0.]
[0. 1.]]
Функция np.diag конструирует диагональную матрицу, используя для заполнения диагонали элементы из переданного ей массива.
diag = np.diag([3.14, 42])
print(diag)
[[ 3.14 0. ]
[ 0. 42. ]]
Кроме того, существует ряд методов, позволяющих создавать массивы из других массивов.
Метод |
Описание |
|---|---|
Присоединение массивов вдоль строк |
|
Присоединение массивов вдоль столбцов |
|
Присоединение массивов “в глубину” |
|
Составление массива из блоков |
Продемонстрируем метод np.block, который позволяет создавать массивы из блоков, в качестве которых могут выступать другие массивы.
print(np.block([[zeros, ones], [eye, diag]]))
[[ 0. 0. 1. 1. ]
[ 0. 0. 1. 1. ]
[ 1. 0. 3.14 0. ]
[ 0. 1. 0. 42. ]]
Более подробно о создании массивов NumPy можно почитать по ссылке.
Арифметические операции над массивами NumPy#
Все основные арифметические операторы (+, -, *, /, //, %, **) перегружены для работы с массивами. Определим скаляр и вектор, чтобы разобраться, какие действия они позволяют выполнять.
x = np.array([3, 13, 42])
alpha = 7
Массив и скаляр#
Если в арифметическом выражении участвуют скаляр и массив, то результатом является массив значений поэлементного применения указанной арифметической операции со скаляром. Т.е., можно, например, умножить массив на число.
print(f"{alpha * x = }")
print(f"{x * alpha = }")
alpha * x = array([ 21, 91, 294])
x * alpha = array([ 21, 91, 294])
Или сложить вектор с числом поэлементно.
print(f"{alpha + x = }")
print(f"{x + alpha = }")
print(horizontal_line)
print(f"{alpha - x = }")
print(f"{x - alpha = }")
alpha + x = array([10, 20, 49])
x + alpha = array([10, 20, 49])
________________________________________________________________________________
alpha - x = array([ 4, -6, -35])
x - alpha = array([-4, 6, 35])
Можно поделить и вектор на число и число на вектор.
print(f"{alpha / x = }")
print(f"{x / alpha = }")
alpha / x = array([2.33333333, 0.53846154, 0.16666667])
x / alpha = array([0.42857143, 1.85714286, 6. ])
Естественно можно делать и все остальные арифметические операции.
print(f"{alpha // x = }")
print(f"{x // alpha = }")
print(horizontal_line)
print(f"{alpha % x = }")
print(f"{x % alpha = }")
print(horizontal_line)
print(f"{alpha ** x = }")
print(f"{x ** alpha = }")
alpha // x = array([2, 0, 0], dtype=int32)
x // alpha = array([0, 1, 6], dtype=int32)
________________________________________________________________________________
alpha % x = array([1, 7, 7], dtype=int32)
x % alpha = array([3, 6, 0], dtype=int32)
________________________________________________________________________________
alpha ** x = array([ 343, -1895237401, 1626129905], dtype=int32)
x ** alpha = array([ 2187, 62748517, -1388900736], dtype=int32)
Note
При возведение в степень в последней ячейке произошло переполнение целого числа.
Массив и массив#
Если в выражении участвует два массива, то они должны быть одинаковой формы, а арифметическая операция все равно применяется поэлементно.
Note
Важно запомнить, что все арифметические операторы выполняют поэлементное преобразование. Это в каком-то смысле является стандартным поведением NumPy и многие другие действия NumPy выполняет поэлементно. Далее рассматривается матричное умножение — принципиально не поэлементная операция.
x = np.array([3, 13, 42])
y = np.array([42, 13, 3])
print(f"{x + y = }")
print(f"{x + y = }")
print(horizontal_line)
print(f"{x * y = }")
print(f"{x / y = }")
print(horizontal_line)
print(f"{x // y = }")
print(f"{x % y = }")
print(horizontal_line)
print(f"{x ** y = }")
x + y = array([45, 26, 45])
x + y = array([45, 26, 45])
________________________________________________________________________________
x * y = array([126, 169, 126])
x / y = array([ 0.07142857, 1. , 14. ])
________________________________________________________________________________
x // y = array([ 0, 1, 14])
x % y = array([3, 0, 0])
________________________________________________________________________________
x ** y = array([ 1914644777, -1692154371, 74088])
Матричное умножение#
Оператор * совершает поэлементное умножение, в том числе и для двухмерных массивов.
ones = np.ones(shape=(2, 2))
eye = np.eye(2)
print(f"{ones}\n*\n{eye}\n=\n{ones * eye} ")
[[1. 1.]
[1. 1.]]
*
[[1. 0.]
[0. 1.]]
=
[[1. 0.]
[0. 1.]]
Чтобы произвести матричное умножение, используется оператор @.
print(f"{ones}\n@\n{eye}\n=\n{ones @ eye} ")
[[1. 1.]
[1. 1.]]
@
[[1. 0.]
[0. 1.]]
=
[[1. 1.]
[1. 1.]]
Note
Оператор @ ввели в python специально для обозначения матричного умножения в NumPy в python 3.5. До этого для представления матриц в NumPy использовался специальный тип numpy, на экземпляры которого оператор * действовал, как оператор матричного умножения. Сегодня разработчики NumPy рекомендуют не пользоваться этим типом в своих программах.
Индексация#
Индексация одномерных массивов ndarray осуществляется очень похоже на индексацию последовательностей python (списков, например).
print(a1D)
print(f"{a1D[0] = }, {a1D[-1] = }")
[1. 2. 3. 4.]
a1D[0] = 1.0, a1D[-1] = 4.0
Индексация многомерных осуществляется несколько с новым синтаксисом. Например, чтобы получить элемент на пересечении i-й строки и j-го столбца двухмерного массива array, используется синтаксис
array[i, j]
print(f"{a2D = }")
print(horizontal_line)
print(f"{a2D[1, 0] = }, {a2D[-1][-1] = }")
a2D = array([[1, 2],
[3, 4]])
________________________________________________________________________________
a2D[1, 0] = 3, a2D[-1][-1] = 4
Если к двухмерному массиву применить индексацию одним числом i, то получится i-я строка.
print(f"{a2D[0] = }, {a2D[-1] = }")
a2D[0] = array([1, 2]), a2D[-1] = array([3, 4])
Всё это в целом распространяется на массивы произвольной размерности. Чтобы получить элемент \(n\)-мерного массива, указывается \(n\) индексов, т.е. по индексу на каждое измерение:
a[i_1, i_2, ..., i_n]
Изменение формы массива#
Можно изменять размерность и форму массива, сохраняя данные исходного массива, но с условием, что общее количество элементов остается (size) неизменным.
A = np.arange(12)
print(A)
[ 0 1 2 3 4 5 6 7 8 9 10 11]
Метод np.ndarray.reshape возвращает новый объект с теми же данными, но в массиве новой формой.
B = A.reshape(4, 3)
print(B)
[[ 0 1 2]
[ 3 4 5]
[ 6 7 8]
[ 9 10 11]]
Метод np.ndarray.resize изменяет форму массива на месте.
A.resize(2, 3, 2)
print(A)
[[[ 0 1]
[ 2 3]
[ 4 5]]
[[ 6 7]
[ 8 9]
[10 11]]]
np.ndarray.ravel вытягивает массив произвольной размерности в одномерный.
A = A.ravel()
print(A)
[ 0 1 2 3 4 5 6 7 8 9 10 11]
View. Разделяемое владение данными и копирование#
На самом деле массивы ndarray устроены чуть сложнее. Массивы ndarray могут разделять одни и те же данные между собой. Массивы можно разделить на два вида: base и view, последний из которых не имеет собственных данных, а ссылается на данные внутри массива base.
baseмассив владеет данными;viewлишь позволяет по-другому на них посмотреть.
Каждый ndarray представляет собой объект, который хранит не только указатель на данные (нечто очень похожее на C массив), но еще и метаданные, говорящие массиву, каким образом интерпретировать эти данные.
Рассмотрим пример. Создадим массив A и убедимся, что он владеет своими данными.
A = np.arange(6)
print(A)
print("Флаги массива A: \n", A.flags)
[0 1 2 3 4 5]
Флаги массива A:
C_CONTIGUOUS : True
F_CONTIGUOUS : True
OWNDATA : True
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
UPDATEIFCOPY : False
Мы создали массив (ndarray) размера 6, который владеет данными [0, 1, 2, 3, 4, 5] типа np.int. Созданный массив мы связали с именем A.
Теперь создадим новый массив B путем изменения формы массива A методом reshape. Убедимся, что он использует те же данные.
B = A.reshape(2, 3)
print(B)
print("Массив B пользуется данными массива A?", B.base is A)
print("Флаги массива B: \n", B.flags)
[[0 1 2]
[3 4 5]]
Массив B пользуется данными массива A? True
Флаги массива B:
C_CONTIGUOUS : True
F_CONTIGUOUS : False
OWNDATA : False
WRITEABLE : True
ALIGNED : True
WRITEBACKIFCOPY : False
UPDATEIFCOPY : False
Итак, массив содержит те же числа, но расположенные уже по строкам матрицы размера \(2 \times 3\).
Напротив флага "OWNDATA" стоит False, т.е. данными он не владеет. Картинка ниже объясняет, что произошло. Создался новый объект с новыми метаданными, который ссылается на тот же массив с данными. Эти новые метаданные указывают, что массив данных следует интерпретировать так, как будто в нём хранится матрица размера \(2 \times 3\), записанная по строкам друг за другом.
Создадим транспонированную матрицу методом transpose и убедимся, что она тоже использует данные исходного массива A.
C = B.transpose()
print(C)
print("Массив C пользуется данными массива A?", C.base is A)
[[0 3]
[1 4]
[2 5]]
Массив C пользуется данными массива A? True
Матрица C — транспонирование матрицы B. Под неё тоже не выделился новый массив с данными, а только лишь новые метаданные.
В данном случае, метаданные указывают, что в массиве хранится матрица размера \(3 \times 2\), которая расположена в памяти таким образом, что первый индекс меняется быстрее второго (т.е. как бы по столбцам).
Продемонстрируем, что изменение элементов любого из этих массивов повлияет на остальные.
C[2, 1] = 42
print(f"{A=}")
print(f"{B=}")
print(f"{C=}")
A=array([ 0, 1, 2, 3, 4, 42])
B=array([[ 0, 1, 2],
[ 3, 4, 42]])
C=array([[ 0, 3],
[ 1, 4],
[ 2, 42]])


