Поиск минимума
Contents
Поиск минимума#
Подмодуль scipy.optimize содержит в себе множество методов для решения задач оптимизации (минимизация, максимизация).
from matplotlib import pyplot as plt
def configure_matplotlib():
plt.rc('text', usetex=True)
plt.rcParams["axes.titlesize"] = 28
plt.rcParams["axes.labelsize"] = 24
plt.rcParams["legend.fontsize"] = 24
plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18
plt.rcParams["text.latex.preamble"] = r"""
\usepackage[utf8]{inputenc}
\usepackage[english,russian]{babel}
\usepackage{amsmath}
"""
configure_matplotlib()
Минимизация скалярной функции одного аргумента#
Функция scipy.optimize.minimize_scalar ищет минимум функции \(f\colon \mathbb{R} \to \mathbb{R}\) при независимой переменной в области \(D\subset\mathbb{R}\), т.е. решает задачу
иными словами задачу поиска \(x^*\in\mathbb{R}\), такого что
import numpy as np
from scipy import optimize
from matplotlib import pyplot as plt
def f(x):
return (x - 2) * x * (x + 2)**2
solution = optimize.minimize_scalar(f)
print(solution)
x = np.linspace(-4, 3, 100)
fig, ax = plt.subplots(figsize=(8, 6), layout="tight")
ax.plot(x, f(x), label=r"$f(x)$")
ax.scatter(solution.x, solution.fun, color="red", label="найденный минимум")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.legend()
fun: -9.914949590828147
message: '\nOptimization terminated successfully;\nThe returned value satisfies the termination criteria\n(using xtol = 1.48e-08 )'
nfev: 15
nit: 11
success: True
x: 1.2807764040333458
<matplotlib.legend.Legend at 0x2a85390ec50>
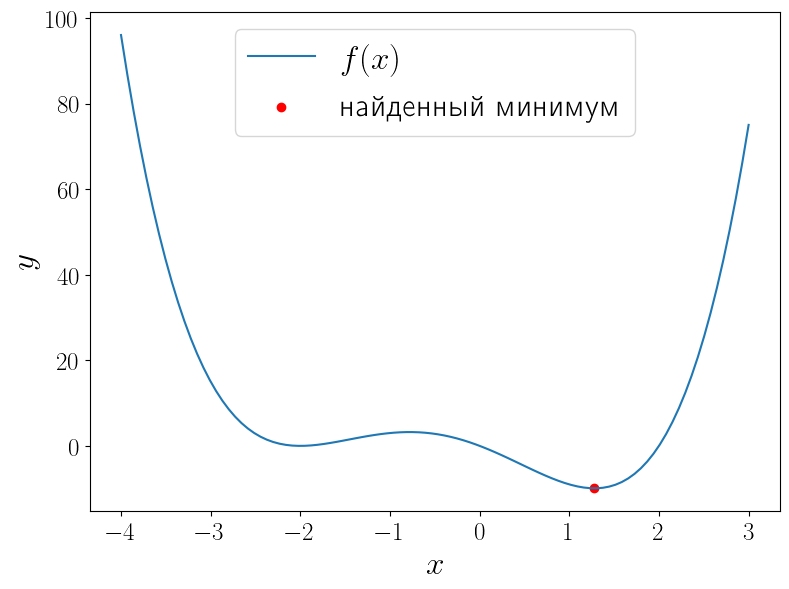
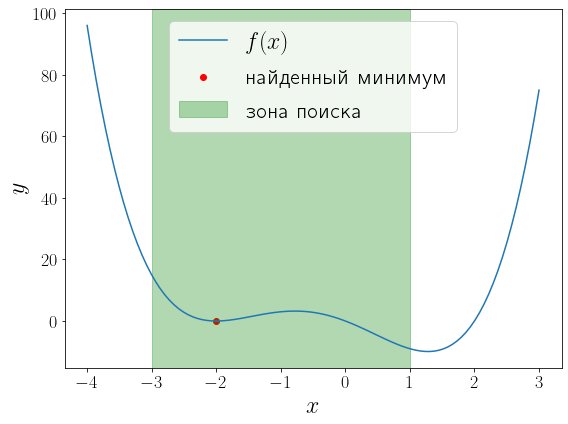
У функции \(f(x) = (x - 1)x(x + 2)^2\) два локальных минимума и функция minimize_scalar вернула из них глобальный. Можно сузить поиск область поиска минимума используя метод bounded.
a, b = -3, 1
solution = optimize.minimize_scalar(f, bounds=(a, b), method="bounded")
fig, ax = plt.subplots(figsize=(8, 6), layout="tight")
ax.plot(x, f(x), label="$f(x)$")
ax.scatter(solution.x, solution.fun, color="red", label="найденный минимум")
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
ax.axvspan(a, b, color="green", alpha=0.3, label="зона поиска")
ax.legend()
<matplotlib.legend.Legend at 0x1fcbc8e9e80>
Минимизация функции многих переменных#
Общий случай#
Функция scipy.optimize.minimize предназначена для минимизации функции многих переменных \(f\colon\mathbb{R}^n\to\mathbb{R}\) при независимой переменной в области \(D\subset\mathbb{R}^n\):
При этом важно определить минимизируемую функцию именно принимающей один векторный аргумент, а не \(n\) скалярных.
В качестве примера рассмотрим поиск минимума функции Розенброка
Её минимум равен 0, который достигается при \(\alpha = \beta = 1\). Для минимизации функции средствами SciPy необходимо определить её в виде функции одного векторного аргумента. Например, если положить, что \(\vec{x}=\begin{pmatrix}x_1 \\ x_2\end{pmatrix}=\begin{pmatrix}\alpha \\ \beta\end{pmatrix}\), то функцию Розенброка можно записать в виде
Именно в таком виде она уже определена в SciPy: rosen. Кроме того в SciPy доступны её градиент rosen_der и матрица Гессе rosen_hess. В ячейке ниже строится график этой функции.
import numpy as np
from scipy import optimize
from matplotlib import pyplot as plt
f = optimize.rosen
def plot_surface():
n_points = 100
x = np.linspace(-1.5, 2.0, n_points)
y = np.linspace(-0.3, 3, n_points)
xx, yy = np.meshgrid(x, y)
X = np.vstack([xx.flatten(), yy.flatten()])
zz = f(X).reshape(n_points, n_points)
levels = np.hstack([np.linspace(0, 200, 25), np.linspace(250, 2000, 25)])
fig, ax = plt.subplots(figsize=(11, 10), layout="tight")
cf = ax.contourf(xx, yy, zz, levels=levels, cmap="coolwarm")
cbar = fig.colorbar(cf)
ax.set_xlabel("$x$")
ax.set_ylabel("$y$")
cbar.set_label("$z$")
ax.scatter([1], [1], marker="*", s=200, color="violet", label="глобальный минимум")
return ax
plot_surface()
<AxesSubplot:xlabel='$x$', ylabel='$y$'>
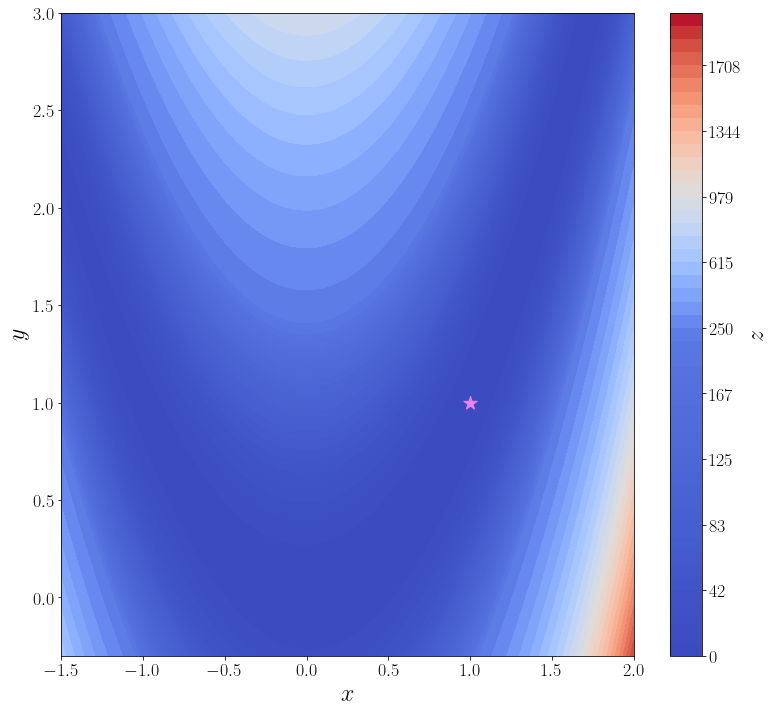
В самой простой своей форме достаточно передать методу optimize.minimize минимизируемую функцию \(f\) и начальное приближение \(x_0\).
solution = optimize.minimize(f, x0=[3, 0])
print(solution)
ax = plot_surface()
ax.scatter(solution.x[0], solution.x[1], color="red", label="найденный минимум")
ax.legend()
fun: 2.0042284826789698e-11
hess_inv: array([[0.49906269, 0.99813029],
[0.99813029, 2.00126989]])
jac: array([-2.75307058e-08, 1.52773794e-08])
message: 'Optimization terminated successfully.'
nfev: 168
nit: 42
njev: 56
status: 0
success: True
x: array([0.99999552, 0.99999104])
<matplotlib.legend.Legend at 0x1fcbfe49a30>
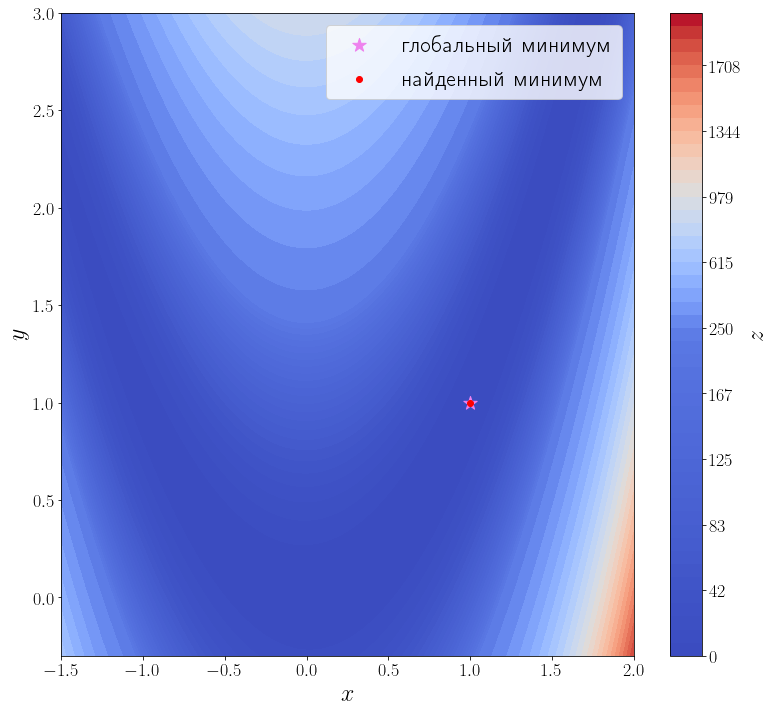
Из возвращаемого значения видно, что метод успешно сошелся и алгоритму потребовалось 42 итерации и 168 вызовов функции f, чтобы сойтись.
Известна первая производная#
Передадим этому методу функцию, вычисляющую матрицу градиент искомой функции. Для этого необходимо использовать параметр jac этой функции.
jacobian = optimize.rosen_der
solution = optimize.minimize(f, x0=[3, 0], jac=jacobian)
print(solution)
ax = plot_surface()
ax.scatter(solution.x[0], solution.x[1], color="red", label="найденный минимум")
ax.legend()
fun: 1.0497719786985556e-20
hess_inv: array([[0.49999817, 1.00001013],
[1.00001013, 2.00505181]])
jac: array([-2.72340728e-09, 1.43485224e-09])
message: 'Optimization terminated successfully.'
nfev: 54
nit: 42
njev: 54
status: 0
success: True
x: array([1., 1.])
<matplotlib.legend.Legend at 0x1fcc1803490>
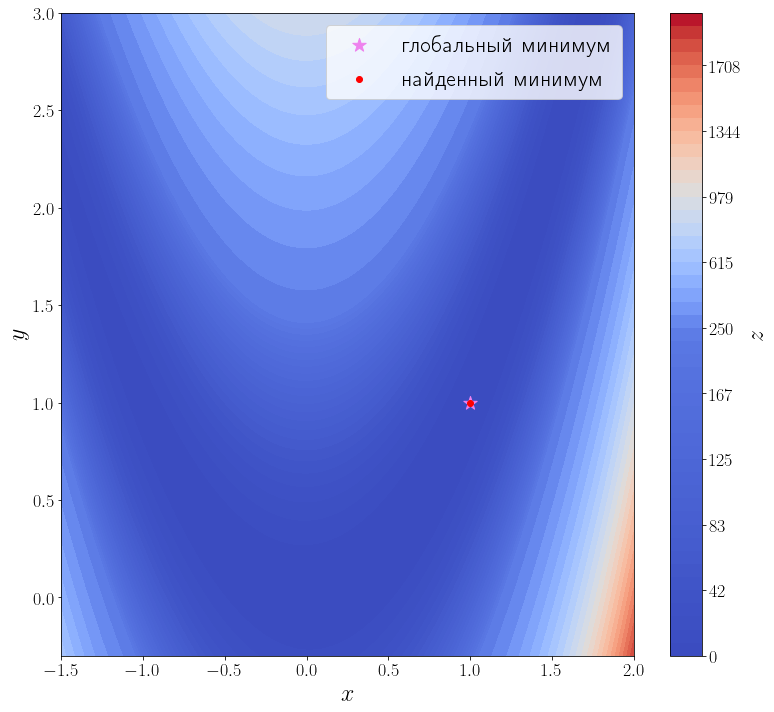
Количество итераций осталось прежним, а количество вызовов функции f снизилось до 35. Это достигается за счет того, что метод минимизации вычисляет производную, вызывая переданную функцию jac, а до этого он её оценивал численно, что требовало дополнительных вызовов f.
Известны первая и вторая производные#
Передадим ещё информацию о второй производной функции f, т.е. матрицу Гессе. Метод минимизации по умолчанию (BFGS) — метод первого порядка, чтобы задействовать матрицу Гессе, необходимо использовать метод второго порядка, например, dogleg.
hessian = optimize.rosen_hess
solution = optimize.minimize(f, [3, 0], method="dogleg", jac=jacobian, hess=hessian)
print(solution)
ax = plot_surface()
ax.scatter(solution.x[0], solution.x[1], color="red", label="найденный минимум")
ax.legend()
fun: 3.514212495812258e-16
hess: array([[ 802.00002985, -400.00000744],
[-400.00000744, 200. ]])
jac: array([ 1.31311361e-07, -4.70576911e-08])
message: 'Optimization terminated successfully.'
nfev: 18
nhev: 14
nit: 17
njev: 15
status: 0
success: True
x: array([1.00000002, 1.00000004])
<matplotlib.legend.Legend at 0x1fcbffeaa90>
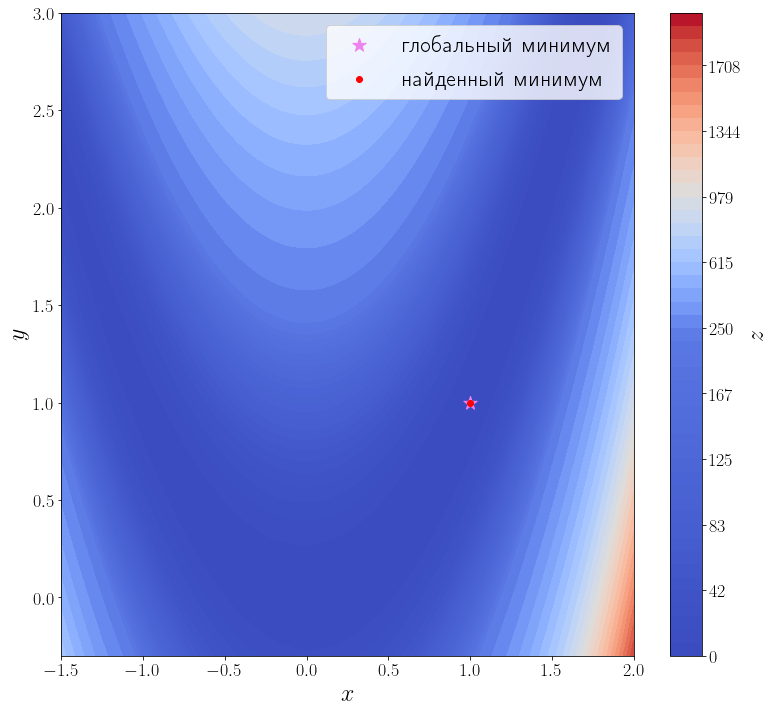
Методу второго порядка потребовалось всего 17 итераций и 18 вызовов функции f, чтобы сойтись.


