Домашнее задание №4

Warning

Это домашнее задание требуется оформить в виде блокнота jupyter. Хостом может выступать как ваш ноутбук, так и удаленный сервер (в том числе и google colab).

В рамках четвертого домашнего задания вам предлагается решить 6 следующих задач:

1. Нормальное распределение;

2. Роза;

3. Вычисление площади методом Монте-Карло;

4. Геометрическая интерпретация плотности вероятности;

5. Состав вселенной;

6. Поверхности.

В рамках каждой задачи от вас потребуется построить график(и). На каждом графике в обязательном порядке должны быть подписаны оси. Если в одних осях отображено несколько зависимостей, то в обязательном порядке должна присутствовать легенда.

К каждой задаче приводится график, который можно использовать в качестве ориентира, но от вас не требуется повторять его в точности.

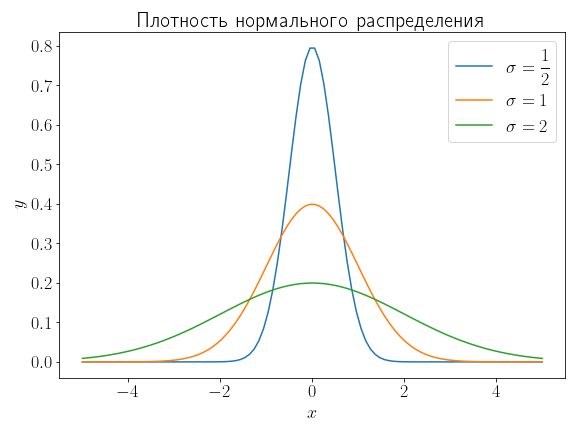
1. Нормальное распределение

Нормальное распределение определяется плотностью вероятности

\[ f(x) = \dfrac{1}{\sigma\sqrt{2\pi}}e^{-\tfrac{(x - \mu)^2}{2\sigma^2}}, \]

где \(\mu\) — математическое ожидание, а \(\sigma\) — среднеквадратичное отклонение. На одном графике (в одних осях) постройте график плотности вероятности при \(\sigma=1\), \(\sigma=\dfrac{1}{2}\) и \(\sigma = 2\) разным цветом. На графике в обязательном порядке должна присутствовать легенда.

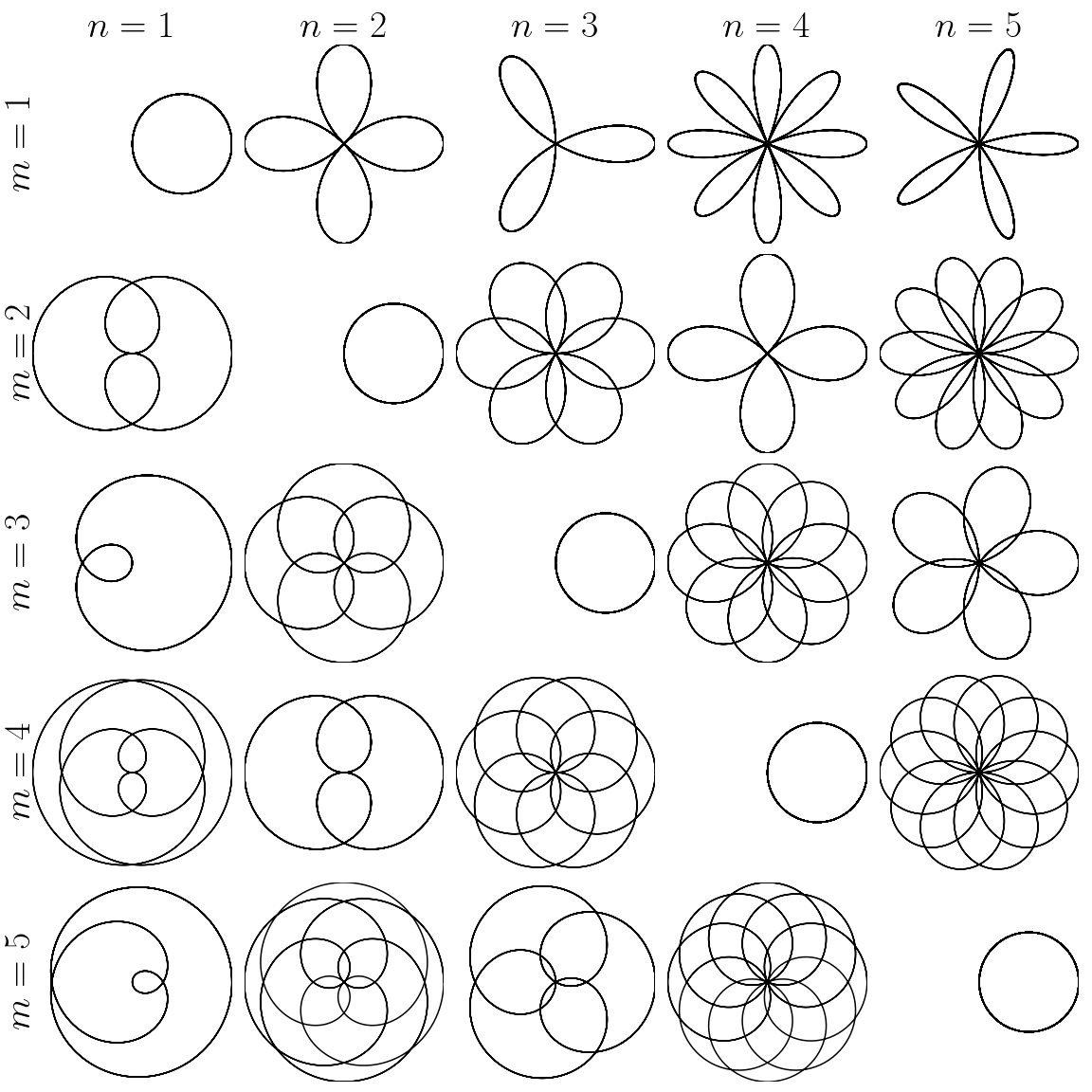
2. Роза

Кривая “роза” задаётся в полярной системе координат уравнением

\[ \rho = a \sin (k\varphi), \]

где \(a\) и \(k\) — постоянные параметры. Пусть \(a = 1\), а \(k=\dfrac{m}{n}\), т.е.

\[ \rho = \sin\left(\dfrac{m}{n}\varphi\right). \]

Ваша задача построить графики такой кривой при \(m=1,\ldots,M\) и \(n=1,\ldots,N\) в виде таблицы, вдоль строк которых сохраняется постоянное значение коэффициента \(m\), а вдоль столбцов — коэффициента \(n\).

3. Вычисление площади методом Монте-Карло

Метод Монте-Карло может быть применен для поиска площади произвольной геометрической фигуры. Пусть геометрическая фигура \(A\) находится внутри прямоугольника \(R\) и требуется найти \(S_A\) — площадь фигуры \(A\).

Сгенерируем случайную точку \((x, y)\) внутри прямоугольника равномерным образом. Тогда согласно геометрическому определению вероятности вероятность \(p_A\), того что эта точка окажется внутри геометрической фигуры \(A\), определяется соотношением

\[ p_A = P(\{(x, y) \in A\}) = \dfrac{S_A}{S_R}, \]

где \(S_R\) — площадь прямоугольника \(R\). Таким образом, чтобы найти \(S_A\), достаточно знать вероятность \(p_A\). Применение метода Монте-Карло заключается здесь в том, чтобы оценить эту самую вероятность эмпирически. Для этого генерируется \(N\) равномерно распределенных внутри прямоугольника \(R\) точек, подсчитывается количество \(n\) точек, оказавшихся внутри фигуры \(a\) и принимается, что если \(N\) достаточно велико, то \(p_A \approx \dfrac{n}{N}\) и формула для оценки площади \(\hat{S}_A\) принимает вид

\[ \hat{S}_A = S_R \dfrac{n}{N}. \]

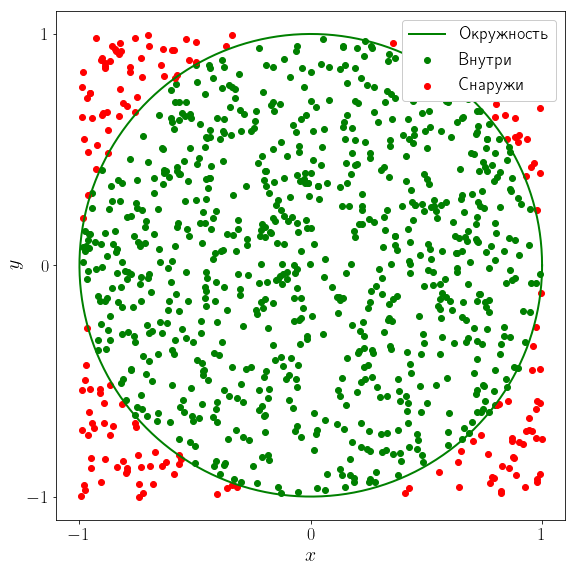
От вас требуется найти площадь единичной окружности.

1. Постройте график окружности.

2. Случайным образом сгенерируйте выборку \(\{(x_1, y_1), \ldots, (x_N, y_N)\}\) из \(N\) точек, равномерно распределенных на квадрате \([-1, 1]^2\). Для этого достаточно сгенерировать \(2N\) чисел, равномерно распределенных на отрезке \([-1, 1]\), и считать, что первая половина из них — \(x\)-координаты точек, а вторая — \(y\)-координаты этих точек.

3. Выяснить, какие из этих точек находятся внутри окружности, а какие снаружи.

4. Нанести всю выборку на график с окружностью в виде диаграммы рассеивания, пометив при этом точки внутри окружности зеленным цветом, а снаружи — красным.

5. Оценить площадь окружности по формуле \(\hat{S} = \dfrac{S_R n}{N} = \dfrac{4 n}{N}\), где \(n\) — количество точек внутри окружности.

6. Сравнить оценку с точным значением \(S=\pi\).

Tip

Генерировать выборку случайных чисел, равномерно распределенных на отрезке [low, high] можно методом numpy.random.uniform.

4. Геометрическая интерпретация плотности вероятности

Пусть непрерывная случайная величина \(\xi\) имеет плотность распределения \(f\colon \mathbb{R} \to \mathbb{R}\), тогда вероятность \(p\) попадания \(\xi\) в интервал \([a, b]\) можно найти по формуле

\[ p = P(\{\xi \in [a, b]\}) = \int_a^b f(x) \, dx. \]

Цель этого задания — проиллюстрировать этот факт.

Перепишем выражение вероятности в следующем виде:

\[ p = \dfrac{b-a}{b-a}\int_a^b f(x) \, dx = (b - a) \underbrace{\dfrac{1}{b-a}\int_a^b f(x) \, dx}_{\overline{f}_{[a, b]}} = (b-a)\overline{f}_{[a, b]}, \]

где \(\overline{f}_{[a, b]}\) — среднее значение функции \(f\) на отрезке \([a, b]\). Из этой формы видно, что вероятность \(p\) попадания \(\xi\) в отрезок \([a, b]\) пропорциональна среднему значению \(f_{[a, b]}\) и длине отрезка \([a, b]\).

Предположим теперь, что имеется \(n\) независимых реализаций случайной величины \(\xi\) и \(\eta\) — случайная величина, которая соответствует количеству реализаций, оказавшихся внутри отрезка \([a, b]\). Тогда

\[ \mathbb{E}\eta = np = n(b-a)\overline{f}_{[a, b]}, \]

т.е. если сгенерировать \(n\) точек из распределения с плотностью \(f\), то ожидаемое количество точек, которые окажутся внутри отрезка \([a, b]\), пропорционально а) количеству точек \(n\); б) среднему значению плотности на этом отрезке \(\overline{f}_{[a, b]}\); в) длине отрезка \(b-a\).

Чтобы это продемонстрировать, от вас требуется:

1. сгенерировать массив из \(n\) нормально распределенных (при нулевом математическом ожидании и единичной дисперсии: \(\mathcal{N}(0, 1)\)) случайных величин;

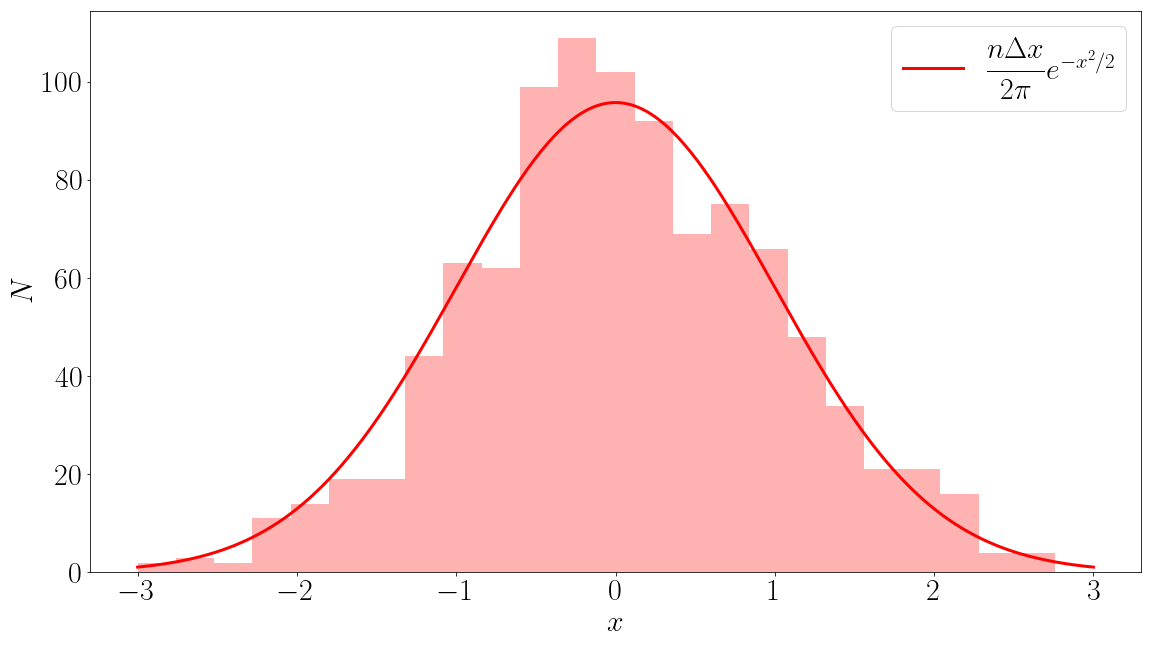
2. построить гистограмму значений этого массива на интервалах равномерной сетки на отрезке \([-3, 3]\) с шагом сетки \(\Delta x\);

3. в тех же осях построить график плотности нормального распределения

\[ f(x) = \dfrac{1}{\sqrt{2\pi}}e^{-x^2 / 2}, \]

домноженной на коэффициент \(n\Delta x\).

Если все верно, то при достаточно большом \(n\) и малом \(\Delta x\) гистограмма должна неплохо аппроксимировать функцию плотности распределения.

Tip

Метод hist по умолчанию строит гистограмму на равномерной сетке из 10 интервалов от минимального до максимального значения. Управлять сеткой можно с помощью опциональных параметров bins и range.

5. Состав вселенной

Согласно википедии вселенная имеет примерно следующий состав.

Вид	Доля, %
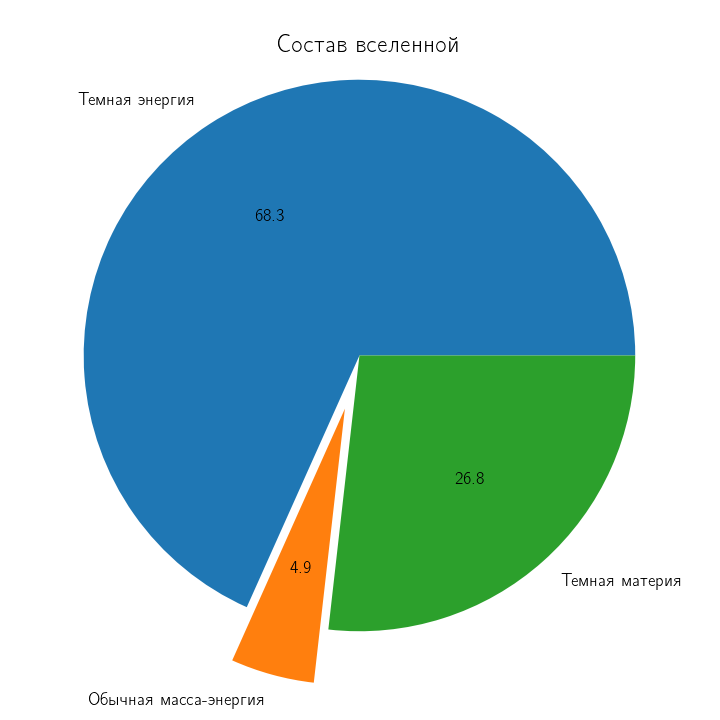
Темная энергия	68.3
Темная материя	26.8
Обычная масса-энергия	4.9

Постройте круговую диаграмму состава вселенной в соответствии с этой таблицей.

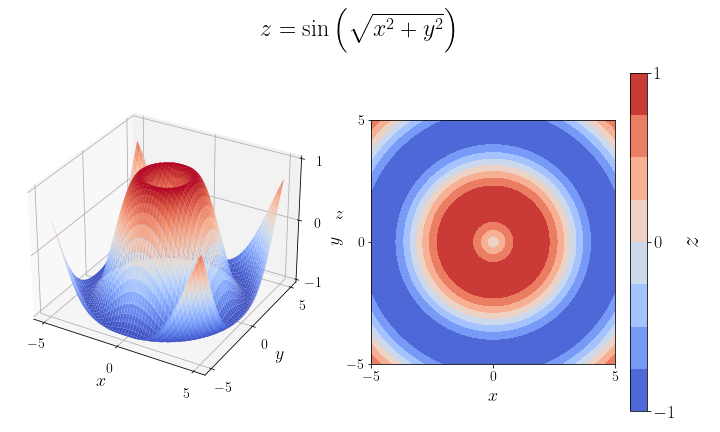
6. Поверхности

Постройте график функции

\[ f(x, y) = \sin\left(\sqrt{x^2 + y^2}\right) \]

при \(x\in[-5, 5]\) и \(y\in[-5, 5]\) в виде поверхности в трехмерных осях, а также в виде линий уровня в двухмерных осях (ось \(Oz\) обозначается цветом).