Обработка сигналов#

Warning

На данной странице под спойлерами находятся ячейки с кодом, реализующим пользовательский интерфейс на основе средств jupyter widgets. На момент написания материалов графический интерфейс не встраивается на сайт при генерации html файлов, так что может потребоваться открытие исходный блокнотов jupyter, например, в google colab (кнопка сверху).

О сигналах#

В рамках данной страницы под сигналом \(x\) будет подразумеваться последовательность чисел \(x[n], \, n=0,\ldots,N-1\), где \(N\) — длинна сигнала, а \(x[n]\in\mathbb{R}\) — значение сигнала в дискретной временной точке \(n\).

Дискретное преобразование Фурье#

Определение#

Пусть имеется сигнал \(x[n], \,n=0,\ldots,N-1\) длинной \(N\). Тогда результат прямымого дискретного преобразования фурье (ДПФ, Discrete Fourier Transform, DPF) определяется выражением

\[ X[k] = \sum_{n=0}^{N-1} x[n] e^{-\tfrac{2\pi i}{N}kn}, \, k=0,\ldots,N-1, \]

где \(X[k]\) — результат прямого дискретного преобразования Фурье, \(i\) — мнимая единица. Прямое преобразование Фурье обратимо и обратное дискретное преобразование Фурье определяется выражением

\[ x[n] = \dfrac1N \sum_{k=0} X[k] e^{\tfrac{2\pi i}{N}kn}, \, k=0,\ldots,N-1. \]

Note

В литературе чаще всего стречается именное такое определение преобразований Фурье, когда перед обратным преобразованием Фурье ставится множитель \(\dfrac1N\), и именно такое определение заложенно во все методы библиотеки scipy. Однако иногда можно встретить и другие нормироваки такого преобразования.

Базис Фурье#

Дискретное преобразование Фурье линейное и по сути дела является разложением по Фурье базису, элементы которого являются комплексными синусоидами

\[ \omega_k[n] = e^{\tfrac{2\pi i}{N}kn} = \cos\left(\dfrac{2\pi}{N}kn\right) + i\sin\left(\dfrac{2\pi}{N}kn\right), \, k=0,\ldots,N-1. \]

С учетом этого факта прямое преобразование Фурье можно записать в матричном виде

\[ X = \mathcal{F}x, \]

где матрица перехода \(\mathcal{F}\) имеет вид.

\[\begin{split} \mathcal{F} = \begin{pmatrix} 1 & 1 & 1 & 1 & \cdots & 1 \\ 1 & \omega & \omega^2 & \omega^3 & \cdots & \omega^{N-1} \\ 1 & \omega^2 & \omega^4 & \omega^6 & \cdots & \omega^{2(N-1)} \\ 1 & \omega^3 & \omega^6 & \omega^9 & \cdots & \omega^{3(N-1)} \\ \vdots & \vdots & \vdots & \vdots & \ddots & \vdots \\ 1 & \omega^{N-1} & \omega^{2(N-1)} & \omega^{3(N-1)} & \cdots & \omega^{(N-1)^2} \end{pmatrix}, \quad \omega = e^{\tfrac{2\pi i}{N}}. \end{split}\]

Столбцы этой матрицы и являются элементами Фурье базиса. Сгенерировать такую матрицу заданного размера можно методом scipy.linalg.dft. В ячейке ниже определяется функция plot_basis_vector для визуализации базисных векторов Фурье, а под ней прокидывается интерактивный интерфейс к этой функции.

import numpy as np
from scipy.linalg import dft
from matplotlib import pyplot as plt


def plot_basis_vector(length: int, index: int): 
    basis_vector = dft(length)[:, index]
    real, imag = basis_vector.real, basis_vector.imag

    fig, axs = plt.subplots(figsize=(16, 8), layout="tight", nrows=2)
    axs[0].stem(real)
    axs[0].set_ylabel("Re$\omega_k[n]$", size=20)
    axs[1].stem(imag)
    axs[1].set_ylabel("Im$\omega_k[n]$", size=20)
    for ax in axs:
        ax.set_xlabel("$n$", size=20)

import ipywidgets as widgets

N = 128
widgets.interact(
    plot_basis_vector,
    length=widgets.fixed(N),
    index=widgets.IntSlider(min=0, max=N-1)
)

<function __main__.plot_basis_vector(length: int, index: int)>

Отсюда видно, что элементы базиса Фурье — синусоиды и косинусоиды разной кратности (гармоники), помещающиеся целое число раз на отрезке \([0, \ldots, N-1]\). Базис Фурье является ортогональным, но не является ортонормированным.

Быстрое преобразование Фурье. `scipy.fft`#

Итак, результатом прямого преобразования Фурье сигнала \(x\) является последовательность комплексных чисел \(X[k]\), которые являются коэффициентами разложения сигнала \(x\) по гармоникам. В модуле scipy.fft определенно множество функций для Фурье-анализа сигналов. Аббревиатура FFT происходит из Fast Fourier Ttransform — быстрое преобразование Фурье (БПФ) — алгоритм ускоренного вычисления дискретного преобразования Фурье. За прямое и обратное быстрое преобразование сигнала произвольной природы (возможно комплексного) отвечают функции fft и ifft, возвращающие комплекснозначный numpy массив всех коэффициентов.

При этом можно показать, что если исходный сигнал \(x\) действительнозначный, то

\[\begin{split} \begin{cases} \mathop{\mathrm{Re}} X[k] = \mathop{\mathrm{Re}} X[N-k], & k=1,\ldots,\left\lfloor\dfrac{N}{2}\right\rfloor, \\ \mathop{\mathrm{Im}} X[k] = -\mathop{\mathrm{Im}} X[N-k], & k=1,\ldots,\left\lfloor\dfrac{N}{2}\right\rfloor. \end{cases} \end{split}\]

Иными словами половину коэффициентов Фурье действительнозначного сигнала можно отбросить. Функция rfft делает именно это: она возвращает только половину необходимых коэффициентов Фурье, а функция irfft осуществляет обратное преобразование Фурье, исходя из предположения, что ей на вход подаётся только половина коэффициентов Фурье, а оставшееся половина восстанавливается из поданных по формулам выше.

Физический смысл#

Модуль \(|X[k]|\) и аргумент \(\angle X[k]\) коэффициента разложения Фурье называют амплитудой и фазой \(k\)-й гармоники. Амплитуда гармоники определяет степень её присутствия в исходном сигнале, а фаза — сдвиг этой гармоники по времени.

Проще всего продемонстрировать смысл коэффициентов разложения Фурье, если сигнал изначально представляет собой линейную комбинацию гармоник. В ячейке ниже определяется функция plot_sinusoid_fft, визуализирующая Фурье-анализ сигнала вида

\[ x[n] = A_1\cos(\dfrac{2\pi}{N}\omega_1(n - b_1)) + A_2\cos(\dfrac{2\pi}{N}\omega_2(n - b_3)) + A_3\cos(\dfrac{2\pi}{N}\omega_3(n - b_3)). \]

В скрытой ячейке ещё ниже прокидывается графический интерфейс, для интерактивного взаимодействия с функцией для визуализации. Подвигав ползунки создайте сигнал из одной гармоники (\(A_1=1\)), и изучите как изменяется спектральное представление сигнала при изменении частоты гармоники (\(\omega_1\)) и (\(b_1\)). Для наглядности рекомендуется использовать метод rfft (флажок real signal) и полярное представления (флажок polar). Флажок prevent phase artifacts предотвращает загрязнение графики с фазами, связанное с неустойчивостью вычислений угла комплексного числа при его близости к нулю.

from scipy.fft import fft, rfft
import matplotlib.gridspec as gridspec

def plot_sinusoid_fft(
    real_signal: bool,
    polar: bool,
    mask_zeros: bool,
    A1: int,
    A2: int,
    A3: int,
    omega1: int,
    omega2: int,
    omega3:int,
    b1: int,
    b2: int,
    b3: int,
): 
    c = 2 * np.pi / N
    t = np.arange(N)
    signal = A1*np.cos(c*omega1*(t-b1)) + A2*np.cos(c*omega2*(t-b2)) + A3*np.cos(c*omega3*(t-b3))
    
    transform_function = rfft if real_signal else fft
    fourier = transform_function(signal)
    real, imag = fourier.real, fourier.imag
    magnitude, phase = np.abs(fourier), np.angle(fourier)
    if mask_zeros:
        phase = np.where(magnitude > 0.0001, phase, 0)
    
    fig = plt.figure(figsize=(16, 8), tight_layout=True)
    gs = gridspec.GridSpec(2, 2)
    ax1 = fig.add_subplot(gs[0, :])
    ax2 = fig.add_subplot(gs[1, 0])
    ax3 = fig.add_subplot(gs[1, 1])
    
    ax1.stem(signal)
    ax2.stem(magnitude if polar else real)
    ax3.stem(phase if polar else imag)
    for ax in (ax1, ax2, ax3):
        ax.set_xlabel("$k$", size=20)
        
    ax1.set_ylabel("$x[k]$", size=20)
    ax2.set_ylabel("$|X[k]|$" if polar else "Re $X[k]$", size=20)
    ax3.set_ylabel(r"$\angle X[k]$" if polar else "Im $X[k]$", size=20)
    
    if polar:
        ax3.set_yticks([-np.pi, -np.pi/2, 0., np.pi/2, np.pi])

from IPython.display import display
from ipywidgets import widgets

N = 64

real_signal = widgets.Checkbox(False, description="real signal")
polar = widgets.Checkbox(True, description="polar")
mask_zeros = widgets.Checkbox(True, description="prevent phase artifacts")
A1 = widgets.IntSlider(min=-5, max=5, description="$A_1$")
A2 = widgets.IntSlider(min=-5, max=5, description="$A_2$")
A3 = widgets.IntSlider(min=-5, max=5, description="$A_3$")
omega1 = widgets.IntSlider(min=0, max=N//2, description="$\omega_1$")
omega2 = widgets.IntSlider(min=0, max=N//2, description="$\omega_2$")
omega3 = widgets.IntSlider(min=0, max=N//2, description="$\omega_3$")
b1 = widgets.IntSlider(min=0, max=N-1, description="$b_1$")
b2 = widgets.IntSlider(min=0, max=N-1, description="$b_2$")
b3 = widgets.IntSlider(min=0, max=N-1, description="$b_3$")

ui = widgets.VBox([
    widgets.HBox([real_signal, polar, mask_zeros]),
    widgets.HBox([A1, omega1, b1]),
    widgets.HBox([A2, omega2, b2]),
    widgets.HBox([A3, omega3, b3]),
])

variables = ("real_signal", "polar", "mask_zeros", "A1", "A2", "A3", "omega1", "omega2", "omega3", "b1", "b2", "b3")
out = widgets.interactive_output(
    plot_sinusoid_fft,
    {varname: globals()[varname] for varname in variables}
)

display(out, ui)

Пример Фурье анализа#

Цикл солнечной активности#

Рассмотрим уже знакомый вам график солнечной активности.

from pathlib import Path
import pandas as pd
from scipy.fft import fftfreq

folder = Path("..", "..") / "assets" / "data" / "signals"
path = folder / "solar_activiry.npy"
year, activity = np.load(path)

fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(year, activity)
ax.set_title("Solar activity by year")
ax.set_xlabel("Year")
ax.set_ylabel("activity")

Text(0, 0.5, 'activity')

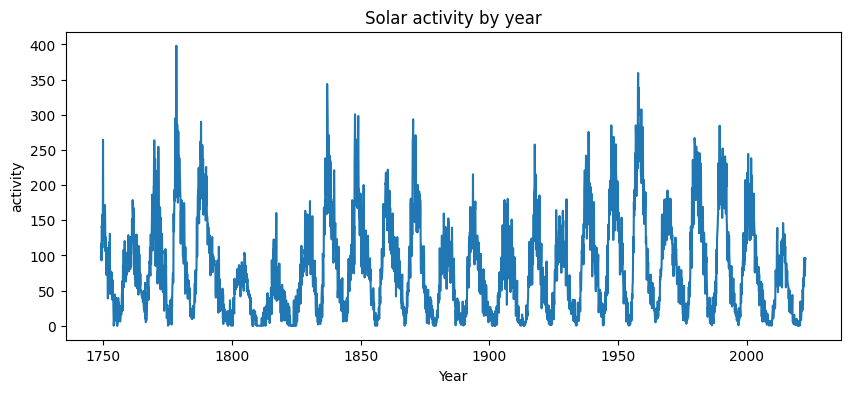
На графике в глаза бросается некоторая сезонность: попробуем определить её период. Для этого вычислим преобразование Фурье и построим график, но по горизонтальное оси отложим не частоту, а период. Так как частота — количество полных колебаний за измеренный диапазон, то период \(T\) соответствующей синусоиды с частотой \(\omega\) можно найти по формуле

\[ T = \dfrac{\text{number of years}}{\omega}. \]

fourier = rfft(activity)
magnitudes = np.abs(fourier)
years_span = year.max() - year.min()
frequency = years_span / np.arange(1, fourier.size)

fig, ax = plt.subplots(figsize=(10, 4))
ax.plot(frequency, magnitudes[1:])
ax.set_xlabel("period [years]")
ax.set_ylabel("magnitude")
ax.set_xscale("log")
ax.axvline(11, color="red", label="11 years")
ax.legend()

<matplotlib.legend.Legend at 0x25c65ccd510>

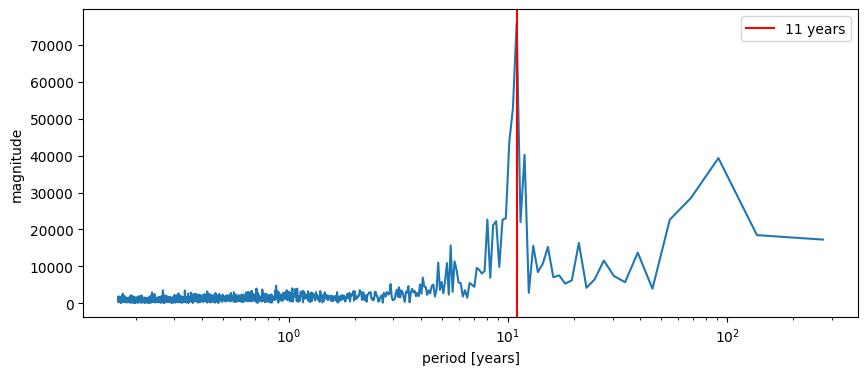
На полученном графике в глаза бросается период в 11 лет, что согласуется с данными из википедии.

Музыкальные инструменты#

На сайте колумбийского университета можно найти короткие записи отдельных нот сыгранных разными инструментами в формате WAV. Человеческий слух может отличить один инструмент от другого без особых проблем. Построим графики этих записей для ноты до и посмотрим, насколько легко отличить инструменты друг от друга визуально.

Note

Для чтения аудиозаписей в формате WAV подходит метод scipy.io.wavfile.read.

from scipy.io import wavfile

instruments = ["piano", "violin", "trumpet", "flute"]

def plot_audio_wave(ax: plt.Axes, instrument: str):
    path = folder / f"{instrument}-C4.wav"
    sample_rate, audio_wave = wavfile.read(path)
    audio_length = audio_wave.size / sample_rate
    timestamps = np.linspace(0, audio_length, audio_wave.size)

    ax.plot(timestamps, audio_wave)
    ax.set_xlabel("time [s]")
    ax.set_ylabel("level")
    ax.set_title(instrument)

fig, axs = plt.subplots(figsize=(10, 16), nrows=4, layout="tight")
for ax, instrument in zip(axs.flatten(), instruments):
    plot_audio_wave(ax, instrument)

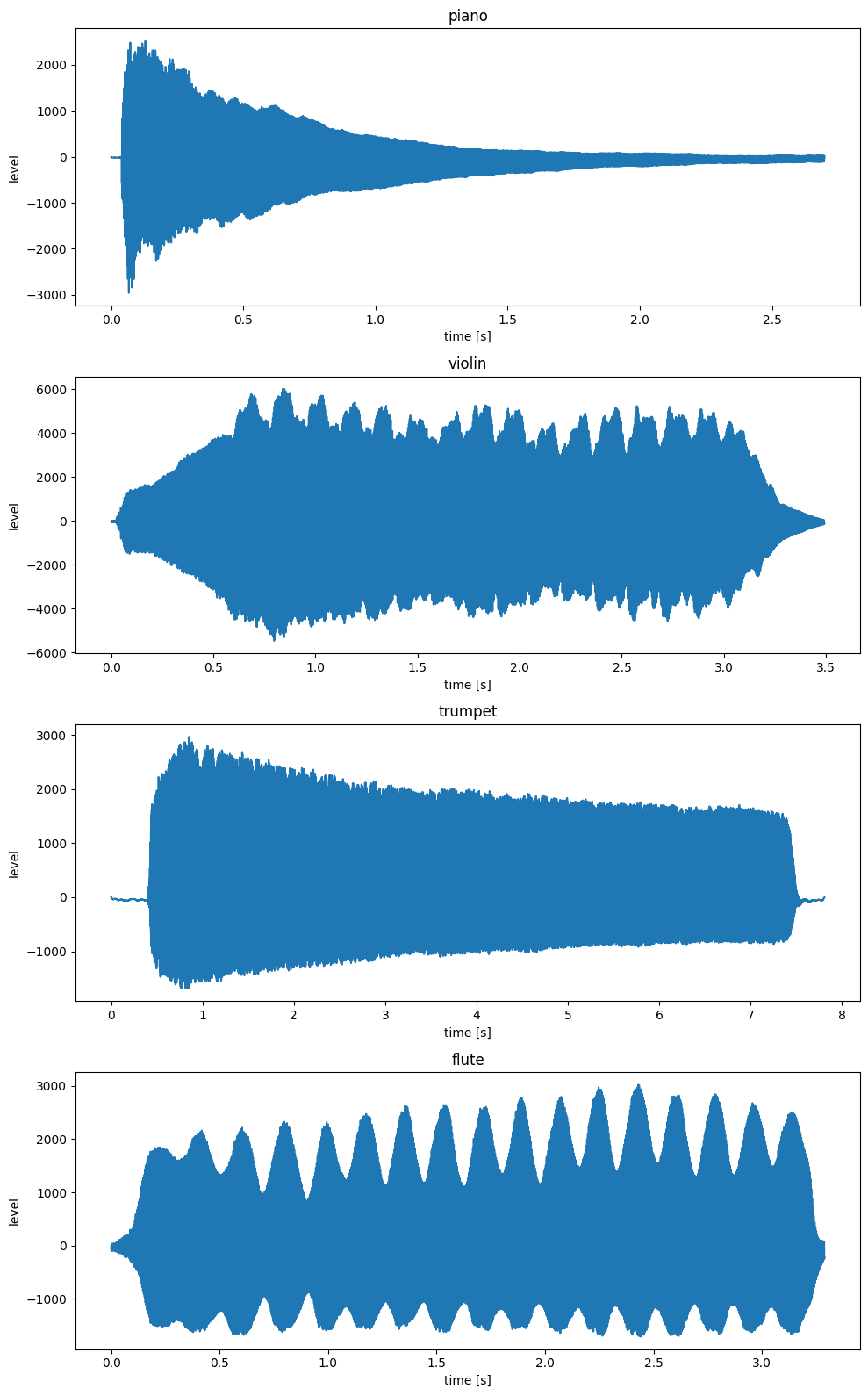
Построенные графики не так уж легко анализировать. Гораздо проще будет анализировать их в частотном спектре. Внизу определяется функция, которая строит частотный спектр и выводит аудиоплеер с записью, а в скрытой ячейке ещё ниже к этой функции прокидывается графический интерфейс.

def music_spectral_analysis(instrument: str, tone: str, fundamental_tone: float):
    path = folder / f'{instrument}-{tone}.wav'
    sample_rate, audio_wave = wavfile.read(path)
    
    fourier = fft(audio_wave)
    magnitudes = np.abs(fourier)
    frequencies = fftfreq(n=audio_wave.size, d=1/sample_rate)
    max_frequency = 2_000
    
    fig, ax = plt.subplots(figsize=(10, 4))
    ax.plot(frequencies, magnitudes)
    ax.set_xticks(np.arange(0, max_frequency, fundamental_tone))
    ax.set_ylim(0, 3 * 1e7)
    ax.set_xlim(-5, max_frequency)
    ax.set_xlabel("frequency [Hz]")
    ax.set_ylabel("level")
    ax.set_title(f"{instrument} {tone}")
    
    audio_player = widgets.Audio.from_file(path, autoplay=False, loop=False)
    return audio_player

output = widgets.interact(
    music_spectral_analysis,
    instrument=widgets.ToggleButtons(
        options=instruments,
        description="Instrument"
    ),
    tone=widgets.ToggleButtons(
        options=["C4", "G4", "C5"],
        description="Tone"
    ),
    fundamental_tone=widgets.fixed(261.63)
)

На построенных графиках видно, что звук распределяется по определенным частотам спектра. Самая низкая из таких частот называется тоном, и именно он определяет высоту звука. Так, например, ноте до из четвертый октавы соответствует частота 261.63 Гц (источник). Остальные, кратные основному тону, частоты называют — обертонами. Распределение звука по обертонам называют тембром, и именно по тембр меняется в зависимости от инструмента, на котором сыграна нота.

Фильтрация низких частот#

ДПФ можно использовать для фильтрации определенных частот в сигнале. Распространенный пример — фильтр нижних частот, который эффективно пропускает частотный спектр сигнала ниже некоторой частоты (частоты среза) и подавляет частоты сигнала выше этой частоты. Такого рода фильтрация иногда применяется в том числе и для фильтрации шумов: несущий информацию сигнал попадает в низкочастотную область, а помехи дают вклад на высоких частотах.

Для реализации такого фильтра в дискретном случае достаточно проделать следующие шаги.

Совершить прямое дискретное преобразование Фурье;
Занулить все коэффициенты получившегося разложения, которые соответствуют частотам выше заданной;
Совершить обратное дискретное преобразование Фурье для разложения с зануленными коэффициентами.

В ячейке ниже определяется функция plot_fourier_filter, визуализирующая действие такого фильтра на зашумленный сигнал в зависимости от пороговой частоты. В скрытой ячейке ещё ниже прокидывается графический интерфейс, для интерактивного взаимодействия с этой функцией. Регулируя положение ползунка, отвечающего за пороговую частоту фильтрации, можно попробовать восстановить исходный сигнал.

from scipy.fft import rfft, irfft

def plot_fourier_filter(signal, noisy_signal, treshold_frequency):
    fourier = rfft(noisy_signal)
    m = fourier.size
    low_freq = irfft(np.where(np.arange(m)>treshold_frequency, 0, fourier))
    high_freq = irfft(np.where(np.arange(m)>treshold_frequency, fourier, 0))
    fig, axs = plt.subplots(figsize=(16, 8), layout="tight", ncols=2, nrows=2)
    titles = ["Исходный сигнал", "Исходный сигнал + шум", "Низкие частоты", "Высокие частоты"]
    ys = [signal, noisy_signal, low_freq, high_freq]
    for ax, y, title in zip(axs.flatten(), ys, titles):
        ax.plot(y)
        ax.set_xlabel("$k$")
        ax.set_ylabel("$y$")
        ax.set_title(title, size=20)

signal = np.load(folder / "triangle.npy")
n = signal.size
noisy_signal = signal + np.random.uniform(0, 0.25, size=n)
widgets.interact(
    plot_fourier_filter,
    signal=widgets.fixed(signal),
    noisy_signal=widgets.fixed(noisy_signal),
    treshold_frequency=widgets.IntSlider(value=0, min=0, max=n-1)
)

<function __main__.plot_fourier_filter(signal, noisy_signal, treshold_frequency)>

Свертка и взаимокорреляция#

Скользящее среднее#

Идея скользящего среднего очень хорошо иллюстрируется в названии операции: окно фиксированной ширины скользит вдоль по массиву и усредняет все попавшие в него значения.

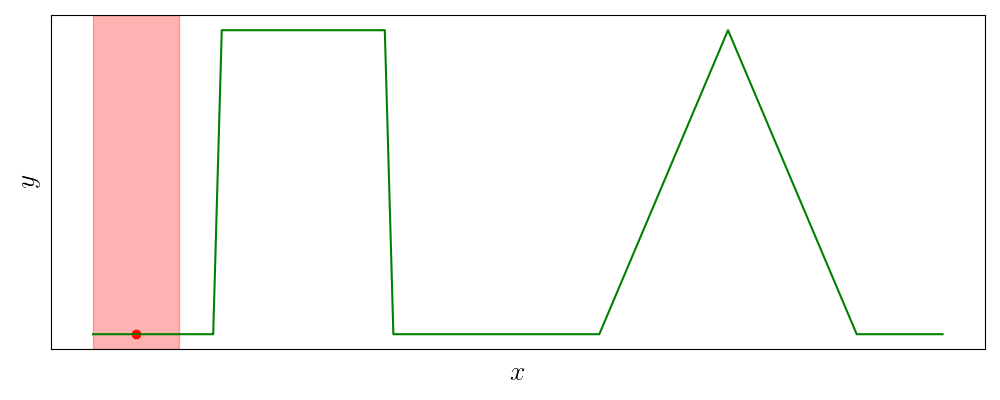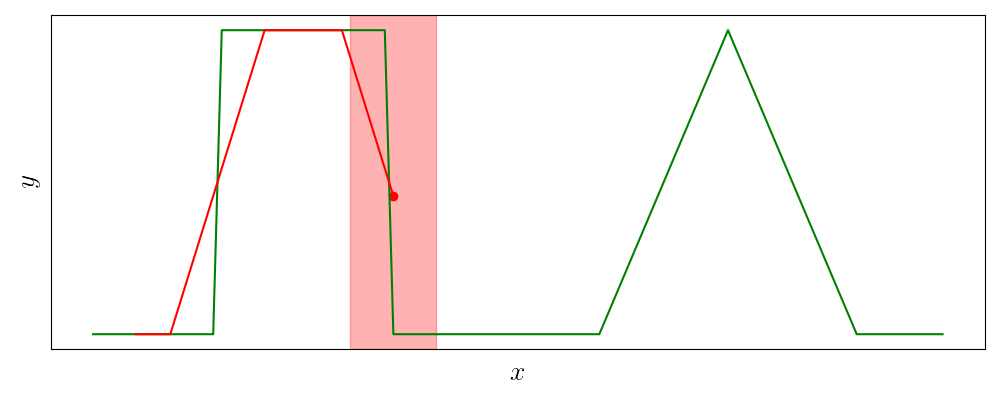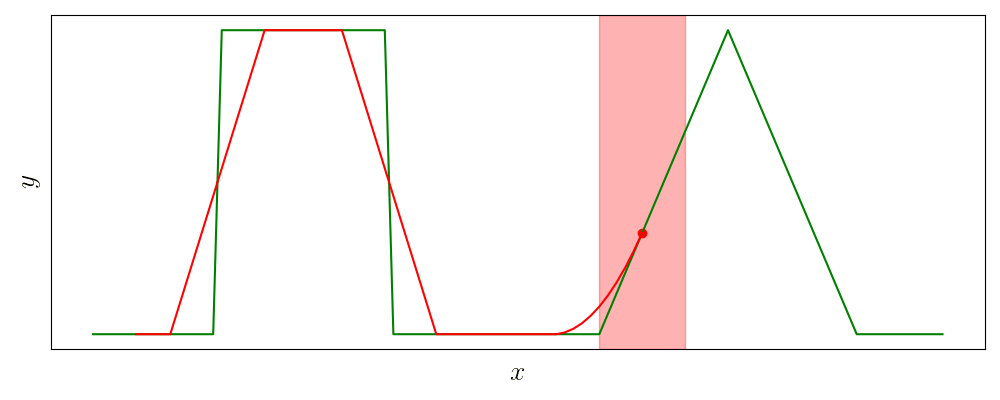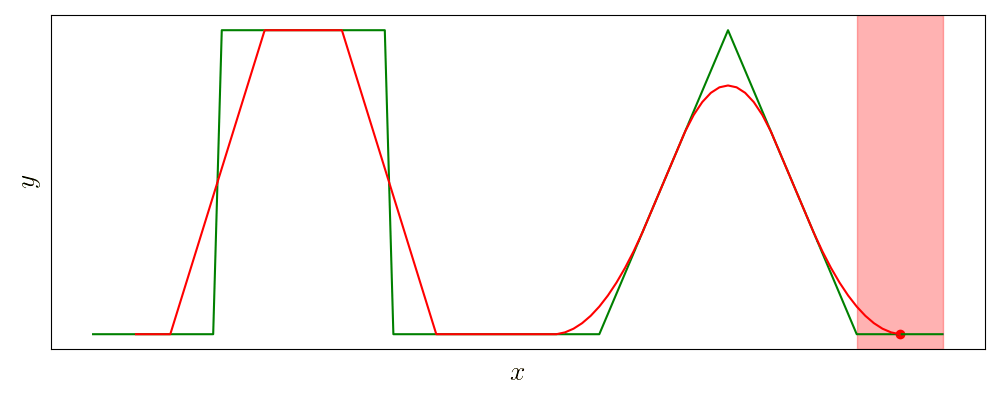
Пусть \(x[i], \, i=0,\ldots,n-1\) — исходный сигнал, тогда результат скользящего среднего \(y\) с окном шириной \(m\) определяется выражением

\[ y[j] = \dfrac{1}{m}\sum_{i=0}^{m - 1} x[i + j], \quad j=0,\ldots,n-m. \]

Анимация ниже иллюстрирует эту формулу при длине исходного сигнала \(n=5\) и ширине окна скользящего окна \(m=3\).

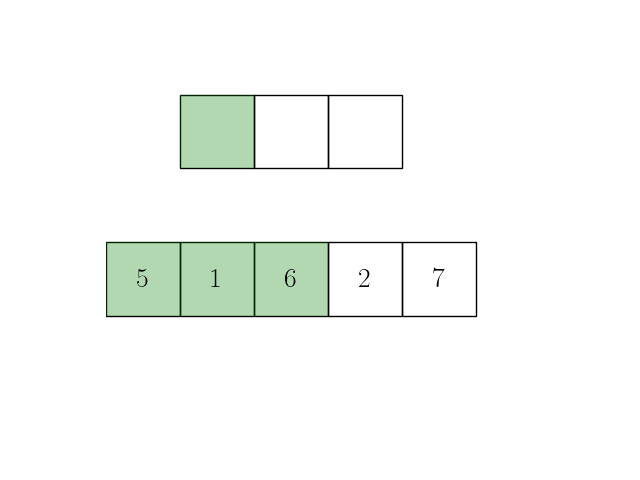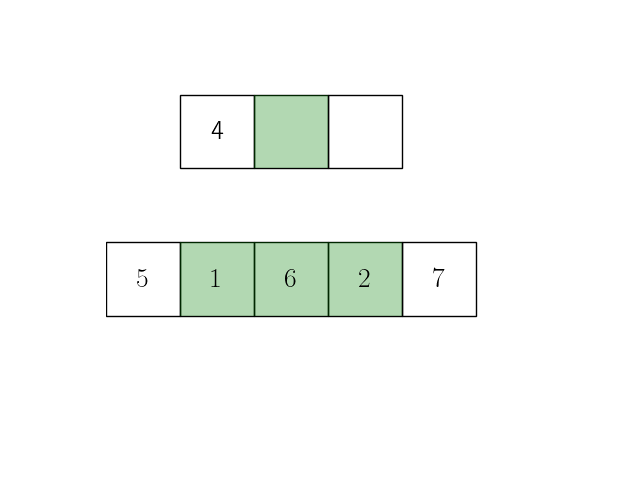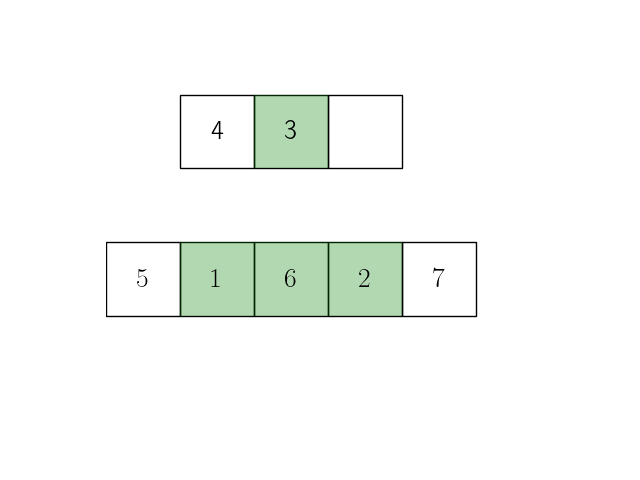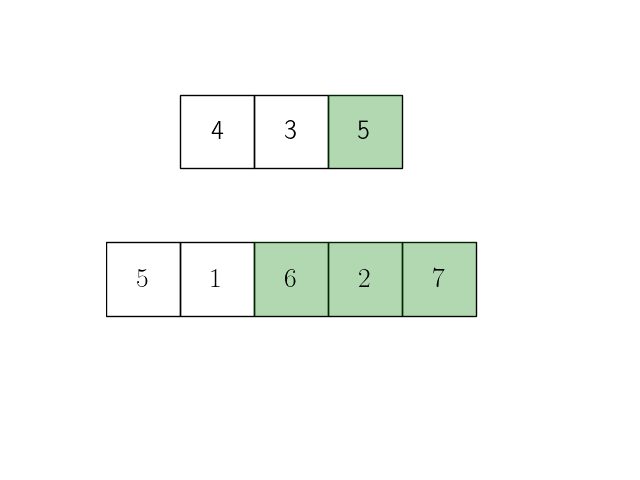
../../_images/moving_average_discrete.gif

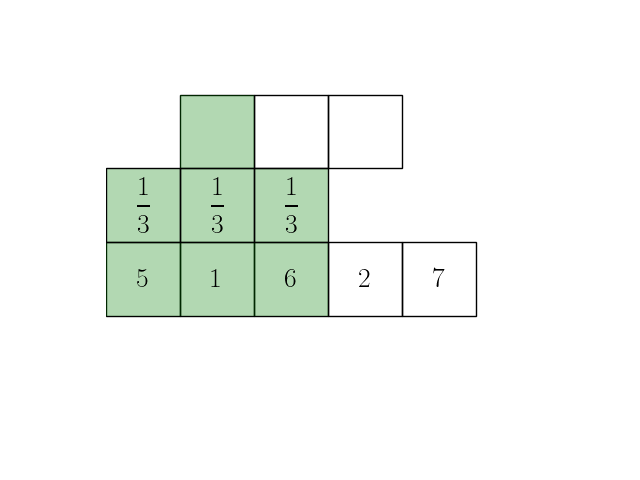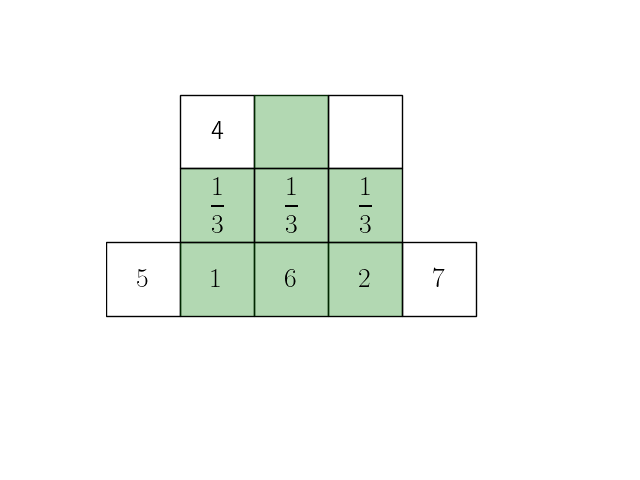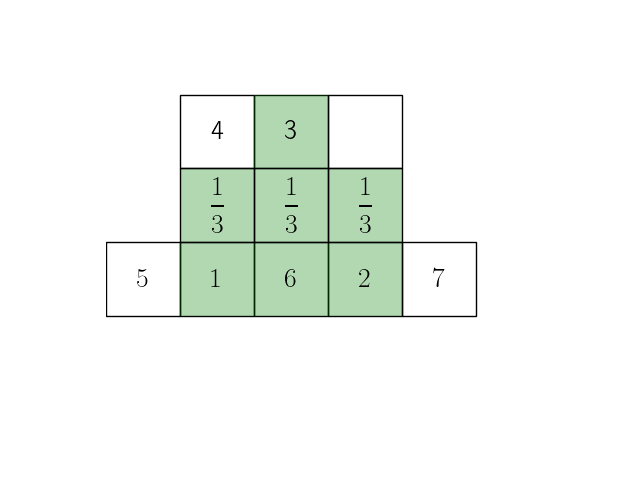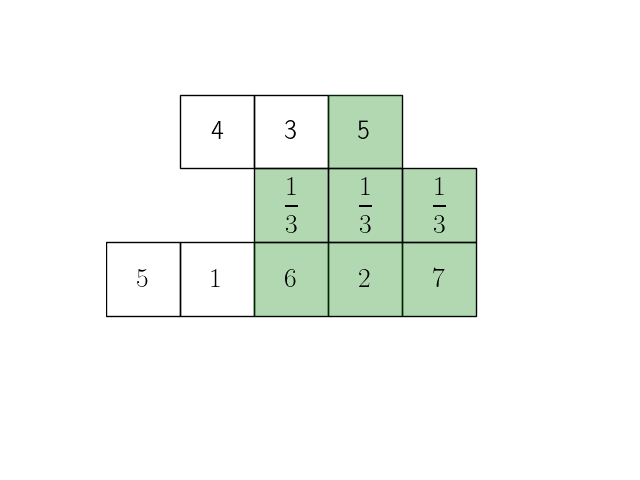
Представим теперь операцию усреднения внутри окна в виде операции взвешенной суммы с коэффициентами \(\dfrac{1}{m}\):

\[ y[j] = \sum_{i=0}^{m - 1} x[i + j] \cdot \dfrac{1}{m}, \quad j=0,\ldots,n-m. \]

../../_images/moving_average_convolve.gif

Свертка `vs` взаимокорреляция#

Свёртка#

Такую операцию можно рассмотреть в качестве частного случая свертки (англ. convolution), которая получится, если значения \(\dfrac{1}{m}\) заменить на набор произвольных коэффициентов \(\omega = \{\omega[i], \, i=1,\ldots,m-1\}\) следующим образом

\[ y[j] = \sum_{i=0}^{m - 1} x[i + j]\cdot\omega[m - i - 1], \quad j=0,\ldots,n-m. \]

Note

Обратите внимание, что в скользящем окне коэффициенты \(\omega[i], \, i=1,\ldots,m-1\) заполнены в обратном порядке.

Набор коэффициентов \(\omega[i], \, i=1,\ldots,m-1\) называют ядром (англ. kernel). Пусть \(x\) — исходный сигнал, \(\omega\) — ядро свертки, тогда результат действия \(y\) свертки с ядром \(\omega\) на сигнал \(x\) будем обозначать \(y = x\circledast \omega\).

Взаимокорреляция#

Если же в скользящем окне заполнить коэффициенты \(\omega[i], \, i=1,\ldots,m-1\) в прямом порядке, то получится операция, которую называют взаимокорреляцией (англ. convolution). В данном случае речь обычно идёт о взаимной корреляции двух сигналов, хотя в определенных можно встретить термин “ядро” и по отношению к \(\omega\) тоже.

\[ y[j] = \sum_{i=0}^{m - 1} x[i + j]\cdot\omega[i], \quad j=0,\ldots,n-m. \]

Реализация в `scipy.signal`#

Вычислить взаимокорреляцию двух сигналов можно методом signal.correlate, а свёртку методом signal.convolve. Оба метода в качестве первых двух параметров принимают два массива, которые представляют два сигнала или сигнал и ядро свёртки.

Однако у обоих методов есть опциональный параметр mode, который отвечает за итоговый размер получившегося массива. Он может принимать один из трех возможных значений: same, valid или full.

Режим `valid`#

В режиме valid окно с ядром скользит только в тех пределах, где ядро полностью накладывается на исходных сигнал.

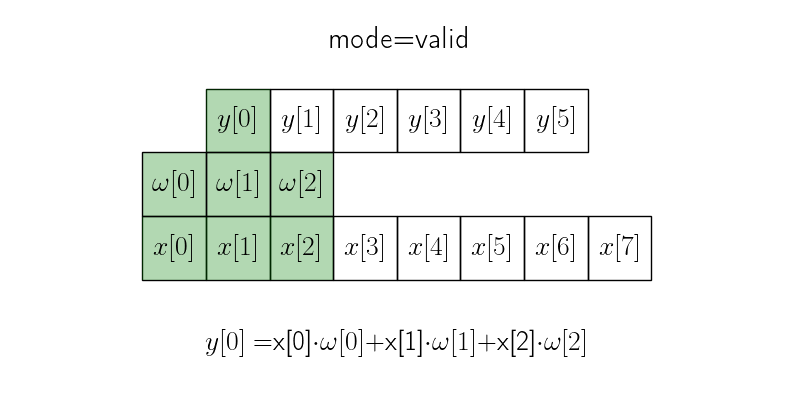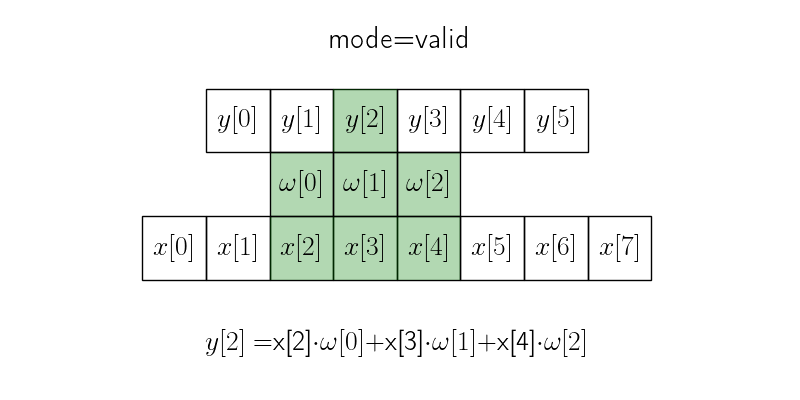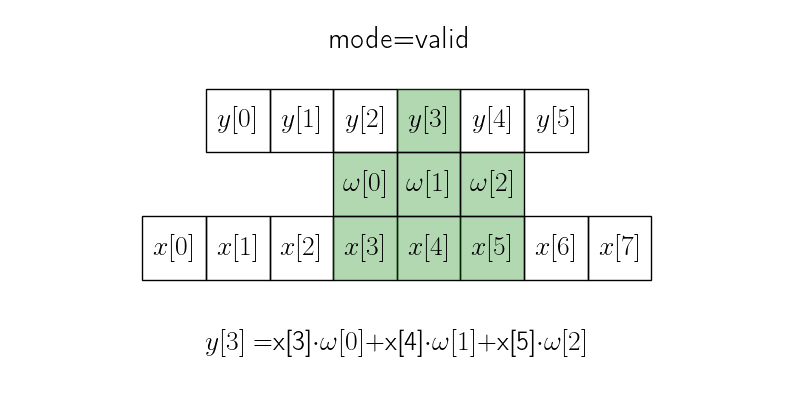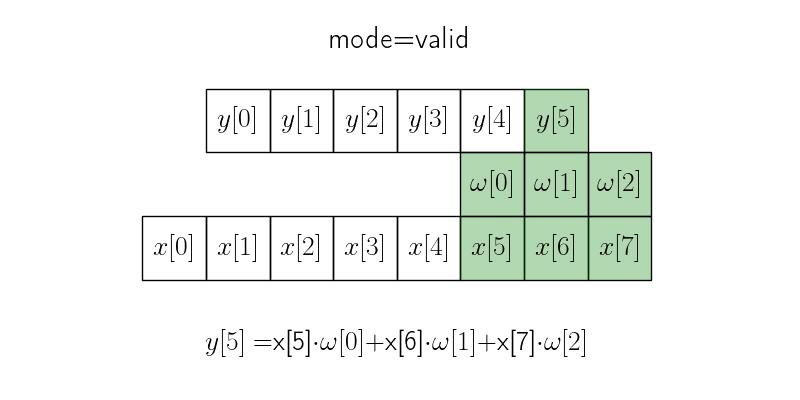
Итоговая длина сигнала получается \(n - m + 1\), где \(n\) — длина исходного сигнала, а \(m\) — размер ядра.

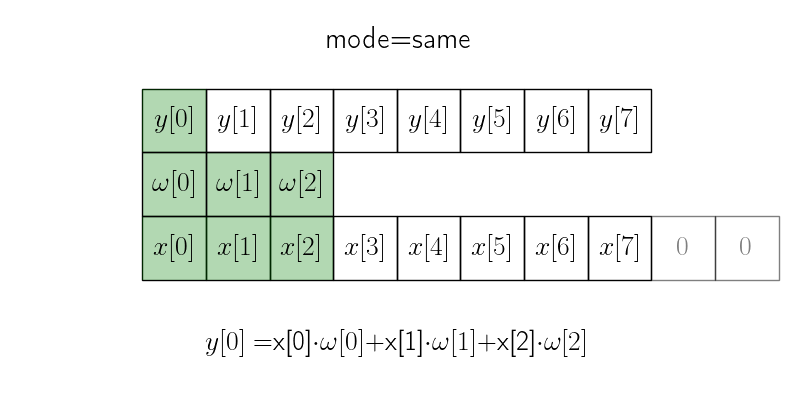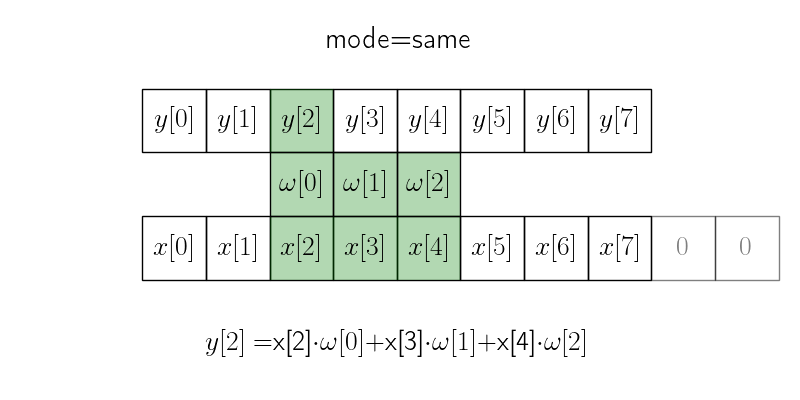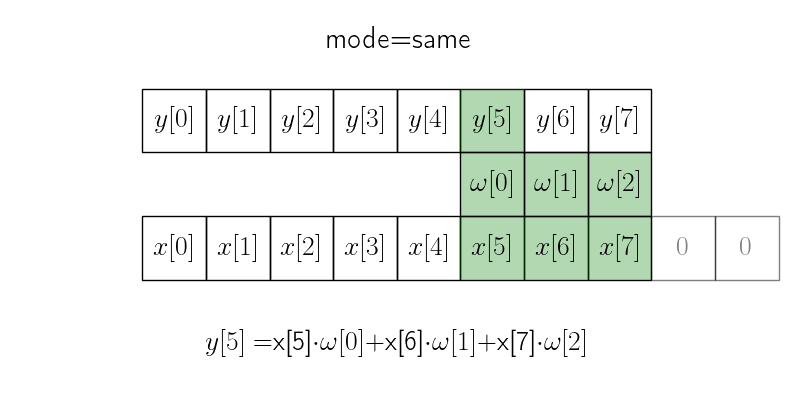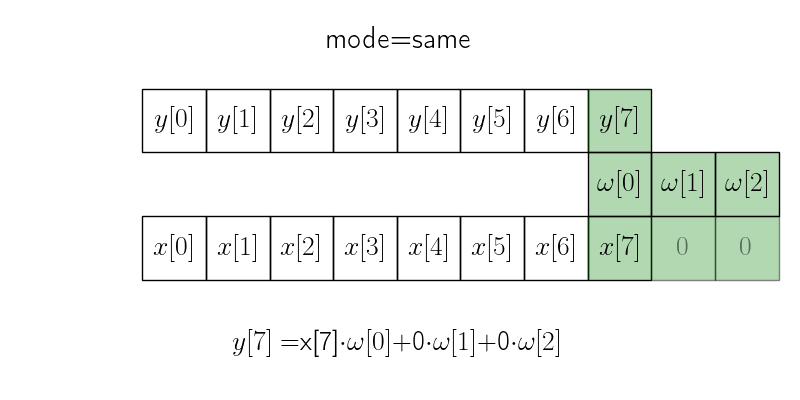
Режим `same`#

В режиме same исходный сигнал \(x\) дополняется необходимым количеством нулей с правой стороны (это количество равно \(m-1\), если \(m\) — размер ядра), чтобы итоговый сигнал имел такую же длину.

Режим `full`#

В режиме full окно с ядром скользит в пределах, где ядро накладывается на исходный сигнал хотя бы одним элементом. Для этого приходится дополнять исходный массив с обеих сторон \(m - 1\) нулями.

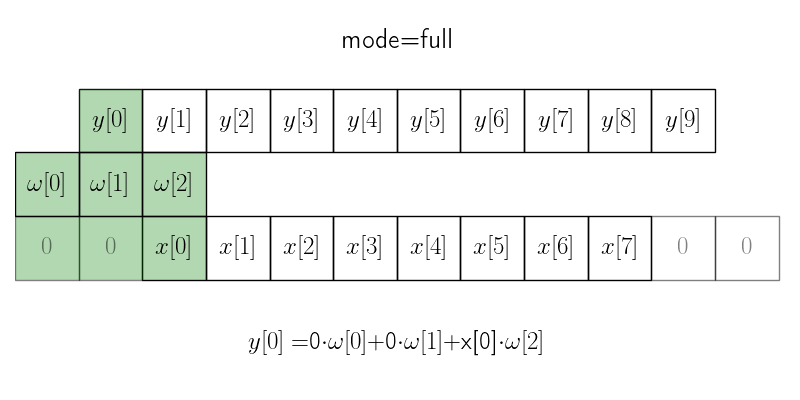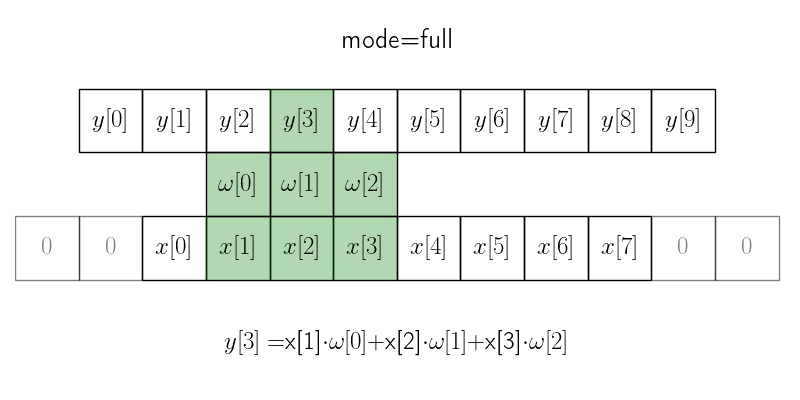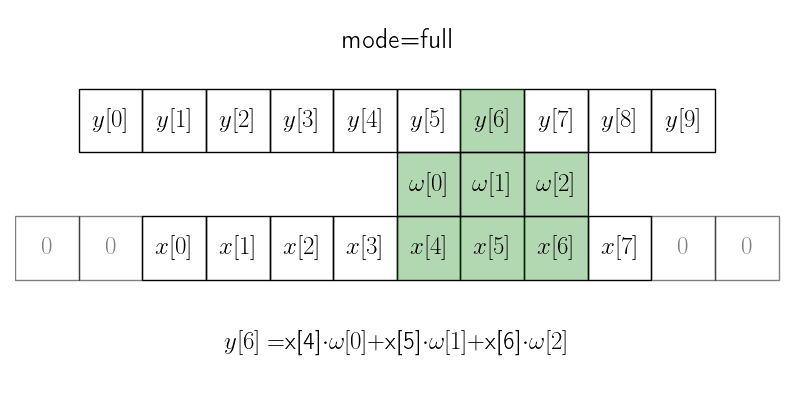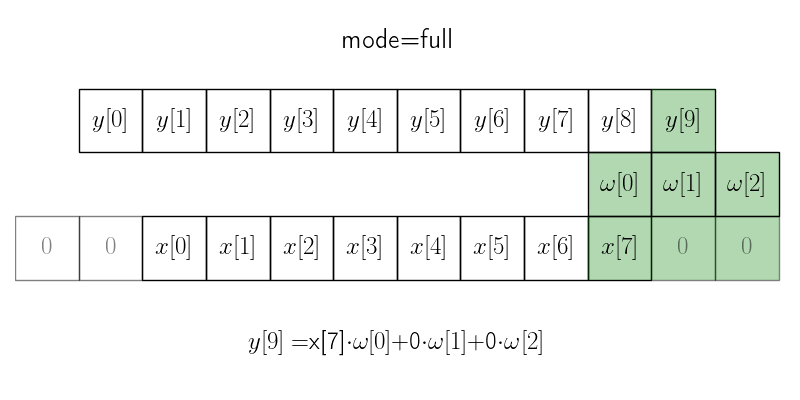
Итоговая длина сигнала получается \(n + m - 1\), где \(n\) — длина исходного сигнала, а \(m\) — размер ядра.

Взаимная корреляция для локализации шаблона#

Операция вычисления взаимной корреляции сигнала \(x\) с шаблонным сигналом \(y\) может быть использована для локализации шаблона внутри этой последовательности, т.к. значение корреляции совпадает с мерой схожести cosine similarity для векторов \(A\) и \(B\)

\[ \cos\theta = \dfrac{A \cdot B}{\|A\|\|B\|}\in{[-1, 1]}. \]

Массив взаимной корреляции совпадает с числителем этой дроби для всех положений шаблона \(y\) внутри сигнала \(x\), если принять, что \(x=A\) и \(y=B\). Чтобы вычислить меру схожести для каждого из положений шаблона внутри сигнала, остаётся только поделить массив взаимной корреляции на соответствующие нормы. Норма массива \(y\) постоянна, а вот норма части массива \(x\), попавшей под шаблон меняется, и для её вычисления требуется произвести оконную операцию.

Внизу приводится функция rolling_cosine_similarity, вычисляющая косинусную меру схожести описанным выше способом, и функция locate_template, визуализирующая способ локализации шаблона на основе такого подхода.

from scipy.signal import correlate
from numpy.linalg import norm
from numpy.lib.stride_tricks import sliding_window_view


def rolling_cosine_similarity(signal, template, eps=1e-10):
    template_norm = norm(template)
    signal_norm = norm(sliding_window_view(signal, template.size), axis=1)
    return correlate(signal, template, mode="valid") / (signal_norm * template_norm + eps)
     
     
def locate_template(signal, template, shift):
    template_x = np.arange(template.size) + shift
    cross_correlation = rolling_cosine_similarity(signal, template)
    correlation = cross_correlation[shift]

    fig, (ax1, ax2) = plt.subplots(figsize=(8, 4), layout="tight", nrows=2)
    ax1.plot(signal, color="green", label="signal")
    ax1.plot(template_x, template, color="red", label="template")
    ax1.set_xlabel("$k$")
    ax1.set_ylabel("$y$")
    ax1.set_xticks(np.arange(0, 256, 28))
    ax1.legend()
    
    ax2.plot(cross_correlation)
    ax2.set_xlabel("lag")
    ax2.set_ylabel("correlation")
    ax2.axhline(0, color="black")
    ax2.set_xticks(np.arange(0, 256, 28))
    ax2.set_title(f"{shift=}, {correlation=:.1f}")
    ax2.stem(shift, correlation, "r")

template = np.load(folder / "template.npy")
signal = np.load(folder / "triangle_step.npy")
widgets.interact(
    locate_template,
    signal=widgets.fixed(signal),
    template=widgets.fixed(template),
    shift=widgets.IntSlider(0, 0, signal.size - template.size)
)

<function __main__.locate_template(signal, template, shift)>

Теорема о свёртке#

Несмотря на то, что взаимная корреляция может показаться более естественной операцией, математики больше любят именно свёртку. Основная причина этому — свойства свёртки, например, теорема о свёртке.

Теорема о свёртке. Пусть \(\mathcal{F}(x)\) и \(\mathcal{F}(y)\) — Фурье образы сигналов одинаковой длины \(x\) и \(y\). Тогда справедливо равенство

\[ \mathcal{F}(x \circledast y) = \mathcal{F}(x) \cdot \mathcal{F}(y), \]

где операция “\(\cdot\)” — операция поэлементного умножения массивов.

Продемонстрируем это свойство на примере вычисления скользящего среднего. Скользящее среднее шириной \(m\) можно представить в качестве свёртки с ядром \(\omega_i = \dfrac{1}{m}\).

signal = np.load(folder / "triangle_step.npy")
n, m = signal.size, 30
filter = np.zeros(n)
filter[:m] = 1 / m

fig, ax = plt.subplots(figsize=(8, 4), layout="tight")
ax.plot(signal, color="green", label="Сигнал")
ax.plot(filter, color="blue", label="Ядро скользящего среднего")
ax.set_xlabel("$k$")
ax.set_ylabel("$y$")
ax.legend()

<matplotlib.legend.Legend at 0x25c778a2470>

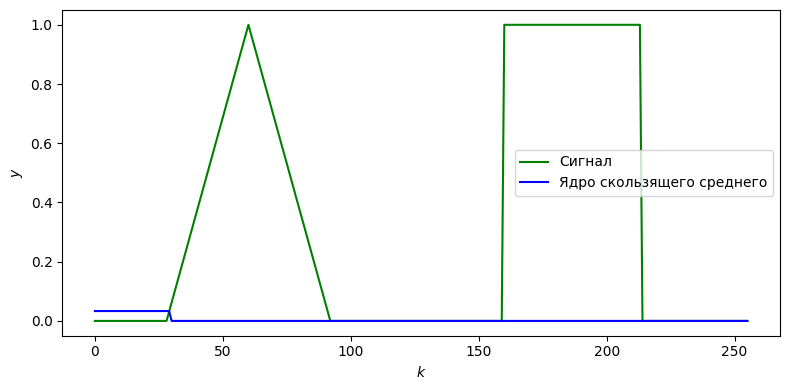
Теперь вычислим результат свёртки с этим ядром в явном виде и опираясь на теорему о свёртке, а затем сравним результаты.

from scipy.signal import convolve

fourier_signal = rfft(signal)
fourier_filter = rfft(filter)
convolution_theorem = irfft(fourier_signal * fourier_filter, n=signal.size)

straightforward = convolve(signal, filter, "full")[:signal.size]

fig, ax = plt.subplots(figsize=(10, 4), layout="tight")
ax.plot(straightforward, color="green", label="Свёртка")
ax.plot(convolution_theorem, color="red", label="Теорема о свёртке", linestyle=" ", marker=".", markersize=3)
ax.set_xlabel("$k$")
ax.set_ylabel("$y$")
ax.legend()

<matplotlib.legend.Legend at 0x25c7ccff910>

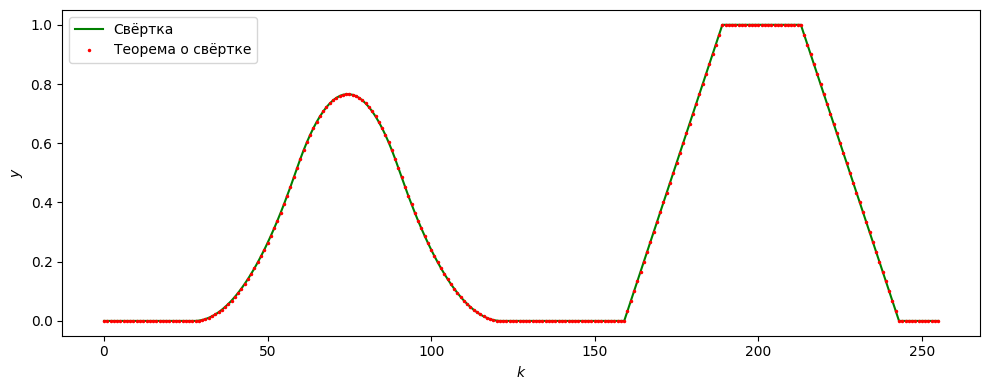
Как видим результаты совпадают. Это позволяет быстро вычислять свертку для длинных сигналов: библиотека scipy тоже использует такой трюк. Кроме того это позволяет анализировать, что делают те или иные фильтры.

Например, ячейка ниже демонстрирует, что скользящее среднее можно считать (неидеальным) фильтром нижних частот.

from scipy.fft import rfft, irfft

def visualize_step_filter(signal, m: int):
    filter = np.zeros(signal.size)
    filter[:m] = 1 / m

    fourier_signal = rfft(signal)
    fourier_filter = rfft(filter)
    filtered_signal = irfft(fourier_signal * fourier_filter, n=signal.size)
    fig, (ax1, ax2) = plt.subplots(figsize=(10, 8), layout="tight", nrows=2)
    ax1.plot(filtered_signal, color="red", label="Сглаженный сигнал")
    ax1.set_xlabel("$k$")
    ax1.set_ylabel("$y$")
    ax1.legend()

    ax2.plot(np.abs(fourier_filter))
    ax2.set_xlabel("frequency")
    ax2.set_ylabel("magnitude")

signal = np.load(folder / "triangle_step.npy")
widgets.interact(
    visualize_step_filter,
    signal=widgets.fixed(signal),
    m=widgets.IntSlider(1, 1, signal.size-1)
)

<function __main__.visualize_step_filter(signal, m: int)>

Практикум по компьютерным технологиям

Обработка сигналов

Contents

Обработка сигналов#

О сигналах#

Дискретное преобразование Фурье#

Определение#

Базис Фурье#

Быстрое преобразование Фурье. `scipy.fft`#

Физический смысл#

Пример Фурье анализа#

Цикл солнечной активности#

Музыкальные инструменты#

Фильтрация низких частот#

Свертка и взаимокорреляция#

Скользящее среднее#

Свертка `vs` взаимокорреляция#

Свёртка#

Взаимокорреляция#

Реализация в `scipy.signal`#

Режим `valid`#

Режим `same`#

Режим `full`#

Взаимная корреляция для локализации шаблона#

Теорема о свёртке#

Практикум по компьютерным технологиям

Обработка сигналов

Contents

Обработка сигналов#

О сигналах#

Дискретное преобразование Фурье#

Определение#

Базис Фурье#

Быстрое преобразование Фурье. scipy.fft#

Физический смысл#

Пример Фурье анализа#

Цикл солнечной активности#

Музыкальные инструменты#

Фильтрация низких частот#

Свертка и взаимокорреляция#

Скользящее среднее#

Свертка vs взаимокорреляция#

Свёртка#

Взаимокорреляция#

Реализация в scipy.signal#

Режим valid#

Режим same#

Режим full#

Взаимная корреляция для локализации шаблона#

Теорема о свёртке#

Быстрое преобразование Фурье. `scipy.fft`#

Свертка `vs` взаимокорреляция#

Реализация в `scipy.signal`#

Режим `valid`#

Режим `same`#

Режим `full`#