Решение ОДУ#

from matplotlib import pyplot as plt


def configure_matplotlib():
    plt.rc('text', usetex=True)
    plt.rcParams["axes.titlesize"] = 28
    plt.rcParams["axes.labelsize"] = 24
    plt.rcParams["legend.fontsize"] = 24
    plt.rcParams["xtick.labelsize"] = plt.rcParams["ytick.labelsize"] = 18
    plt.rcParams["text.latex.preamble"] = r"""
    \usepackage[utf8]{inputenc}
    \usepackage[english,russian]{babel}
    \usepackage{amsmath}
    """

configure_matplotlib()

Подмодуль scipy.integrate содержит в себе множество методов решения систем обыкновенных дифференциальных уравнений (ОДУ, ordinary differential equation, ODE).

Т.к. везде ниже будут строиться графики полученного и точного решений уравнения, определим функцию для построения графиков этих решений.

from matplotlib import pyplot as plt


def plot_solution(ax, x, exact_sol, sol_x, sol_y, xlabel="$t$"):
    ax.plot(x, exact_sol(x), color="green", label="Точное решение")
    ax.scatter(sol_x, sol_y, color="red", marker=".", label="Приближенное решение")
    ax.set_xlabel(xlabel)
    ax.set_ylabel("$y$")
    ax.legend()

Задача Коши#

Функция scipy.integrate.solve_ivp (solve initial value problem) позволяет численно решать задачу Коши вида

\[\begin{split} \begin{cases} \dfrac{dy}{dt} = f(t, y), \\ y(t_0) = y_0. \end{cases} \end{split}\]

Уравнение первого порядка#

В качестве самого простого примера решим уравнение

\[\begin{split} \begin{cases} y' = y, \\ y(0) = 1, \end{cases} \end{split}\]

точное решение которого \(y=e^t\).

Чтобы численно решить это уравнение средствами SciPy, необходимо определить функцию правой части (f(t, y) в ячейке ниже), задать начальное значение \(y(0)\) в виде списка из одного элемента (y_0 в ячейке ниже), а также задать интервал независимой переменной, на которой необходимо решить дифференциальное уравнение.

import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt


def f(t, y):
    return y

def exact_solution(t):
    return np.exp(t)

y_0 = [1]
t_0 = 0
t_final = 3
solution = integrate.solve_ivp(f, (t_0, t_final), y_0)
print(solution)

  message: 'The solver successfully reached the end of the integration interval.'
     nfev: 26
     njev: 0
      nlu: 0
      sol: None
   status: 0
  success: True
        t: array([0.        , 0.10001999, 1.06609106, 2.30431769, 3.        ])
 t_events: None
        y: array([[ 1.        ,  1.10519301,  2.9040598 , 10.01740317, 20.08580546]])
 y_events: None

Метод возвращает структуру со сравнительно большим количеством полей, из которых можно получить отладочную информацию о сходимости алгоритма, а также получить приближенную оценку \(\tilde{y}(t)\) в наборе точек \(\{t_i,\,i=1,\ldots,n\}\).

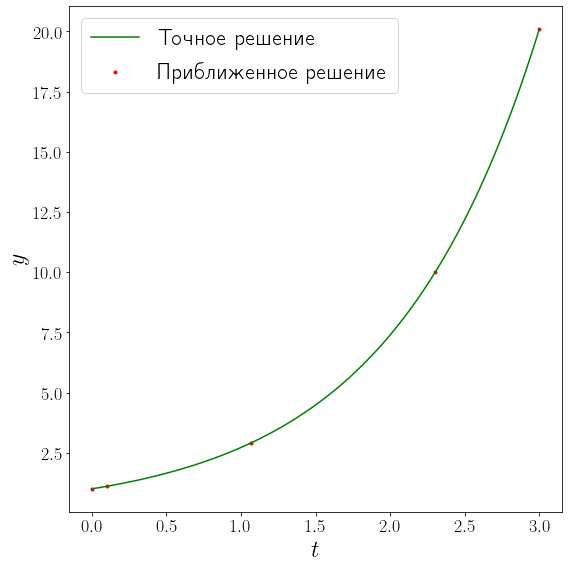
fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
x = np.linspace(t_0, t_final, 100)
plot_solution(ax, x, exact_solution, solution.t, solution.y[0])

Note

Хоть правая часть уравнения и не зависит явным образом от \(t\), функция f(t, x) все равно объявляется с первым параметром t.

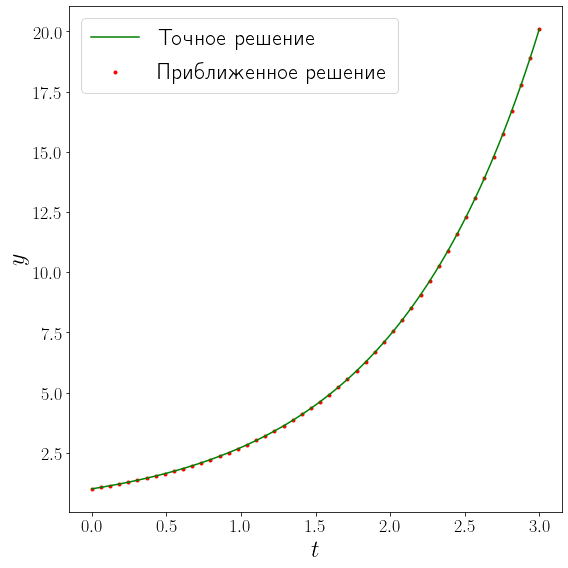
Для данного уравнения функция scipy.integrate.solve_ivp выдала решение, содержащее совсем небольшое количество точек, так как метод быстро сошелся. Параметром t_eval можно в явно виде задать сетку, в узлах которой требуется получить оценку точного решения.

solution = integrate.solve_ivp(f, (t_0, t_final), y_0, t_eval=np.linspace(t_0, t_final, 50))

fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_solution(ax, x, exact_solution, solution.t, solution.y[0])

Уравнения высшего порядка#

Предполагается, что в общем случае \(y=y(t)\) является векторной и решается система обыкновенных дифференциальных уравнений.

\[\begin{split} \begin{cases} \dot{y}_1 = f_1(t, y_1, \cdots, y_n), \\ \cdots \\ \dot{y}_n = f_n(t, y_1, \cdots, y_n), \\ y_1(t_0) = y_{1,0}, \\ \cdots \\ y_n(t_0) = y_{n,0}. \end{cases} \end{split}\]

Если имеется дифференциальное уравнение высшего порядка разрешенное относительно старшей переменной вида

\[ y^{(n)} = f(t, y, y', \ldots, y^{(n-1)}), \]

то необходимо свести его к системе из \(n\) уравнение первого порядка.

В качестве примера решим уравнение

\[\begin{split} \begin{cases} z'' + z = 0, \\ z(0) = 0, \\ z'(0) = 1, \end{cases} \end{split}\]

точное решение которого — \(z = \sin t\). Чтобы его решить, необходимо свести уравнение к системе двух дифференциальных уравнений первого порядка. Введём обозначения \(y_1(t) = z(t)\) и \(y_2(t) = z'(t)\), тогда систему выше можно переписать в виде

\[\begin{split} \begin{cases} y_1'(t) = y_2(t), \\ y_2'(t) = -y_1(t), \\ y_1(0) = 0, \\ y_2(0) = 1. \end{cases} \end{split}\]

В таком случае функция правой части уравнения должна принимать на вход вектор \(y\) и возвращать вектор производны \(y'=f(t, y)\) в виде списка или массива NumPy.

def exact_solution(t):
    return np.sin(t)

def f(t, y):
    return [
        y[1], 
        -y[0]
        ]

y_0 = [0, 1]
t_0 = 0
t_final = np.pi
t_eval = np.linspace(0, np.pi, 10)

solution = integrate.solve_ivp(f, (t_0, t_final), y_0, t_eval=t_eval)
print(solution)

  message: 'The solver successfully reached the end of the integration interval.'
     nfev: 44
     njev: 0
      nlu: 0
      sol: None
   status: 0
  success: True
        t: array([0.        , 0.34906585, 0.6981317 , 1.04719755, 1.3962634 ,
       1.74532925, 2.0943951 , 2.44346095, 2.7925268 , 3.14159265])
 t_events: None
        y: array([[ 0.00000000e+00,  3.42054448e-01,  6.42796558e-01,
         8.66269432e-01,  9.85009559e-01,  9.84744759e-01,
         8.66190242e-01,  6.42630108e-01,  3.41454338e-01,
        -5.87748431e-04],
       [ 1.00000000e+00,  9.39714990e-01,  7.66028577e-01,
         5.00009935e-01,  1.73634556e-01, -1.73906214e-01,
        -5.00472507e-01, -7.66382176e-01, -9.39862784e-01,
        -9.99961909e-01]])
 y_events: None

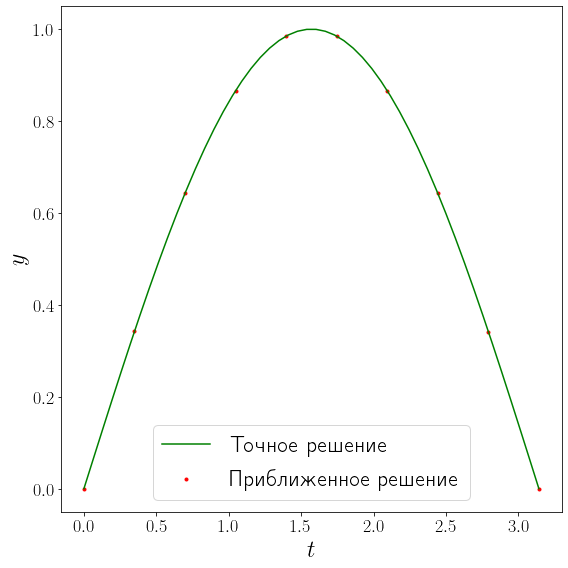
В решении \(y\) тоже возвращается в виде массива из \(n\) строк и \(m\) столбцов, где \(n\) — порядок системы уравнений, а \(m\) — количество точек, в которых построена оценка решения. В данном примере первая строка массива соответствует искомой зависимости \(y_1(t)=z(t)\), а вторая строка — \(y_2(t)\), которая соответствует производной решения \(z'(t)\).

x = np.linspace(0, np.pi, 50)
fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_solution(ax, x, exact_solution, solution.t, solution.y[0])

Выбор метода решения ОДУ#

Решение таких систем ОДУ отнюдь не тривиально. Разработано множество методов их решения и ряд из них “зашит” в подмодуле scipy.integrate, среди которых:

Явные ме́тоды Ру́нге — Ку́тты 2-го (RK23), 4-го (RK45) и 8-го (DOP853) порядков;
Неявный метод Руне — Кутты 5-го порядка Radau;
Неявные методы BDF и LSODA.

Основным критерием выбора является жесткость системы ОДУ: явные методы плохо проявляют себя на жестких системах. SciPy рекомендует использовать по умолчанию метод RK45 и если он плохо/долго сходится переключаться на метод Radau иди BDF.

Краевая задача#

Функция scipy.integrate.solve_bvp (solve boundary value problem`) предназначена для решения системы ОДУ с краевыми условиями

\[\begin{split} \begin{cases} \dfrac{dy}{dx} = f(x, y), \\ y(a) = y_a, \\ y(b) = y_b. \end{cases} \end{split}\]

В качестве аргументов функция solve_bvp принимает:

функцию f, задающую правую часть уравнения,
функцию bc (boundary condition), задающую невязку для граничных условий,
массив x, определяющий сетку значений независимой переменной \(x\),
массив y, задающий “догадку” об итоговом решении \(y = y(x)\).

Функция bc должна принимать на вход \(y(a)\) и \(y(b)\) (векторные величины в общем случае) и возвращать вектор невязки на граничных условиях.

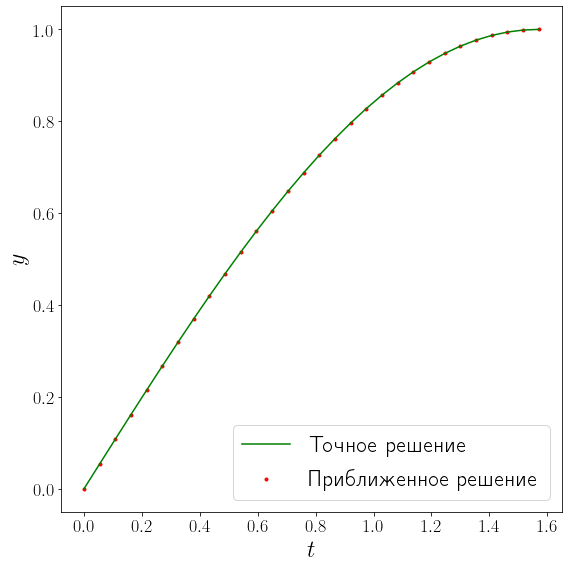
В качестве примера решим последнюю систему,

\[\begin{split} \begin{cases} z'' + z = 0, \\ z(0) = 0, \\ z(\dfrac{\pi}{2}) = 1, \end{cases} \end{split}\]

но с граничными условиями на отрезке \(x \in [0, \frac{\pi}{2}]\). Как и в случае задачи Коши здесь потребуется свести уравнение второго порядка к системе из двух уравнений первого порядка.

\[\begin{split} \begin{cases} y_1'(t) = y_2(t), \\ y_2'(t) = -y_1(t), \\ y_1(0) = 0, y_1(\dfrac{\pi}{2}) = 1. \end{cases} \end{split}\]

import numpy as np
from scipy import integrate
from matplotlib import pyplot as plt


def boundary_residual(ya, yb):
    return np.array([
        ya[0] - 0, 
        yb[0] - 1
        ]) 


a, b = 0, np.pi/2
N = 30
x = np.linspace(a, b, N)
y_guess = np.zeros((2, N), dtype=float)

sol = integrate.solve_bvp(f, boundary_residual, x, y_guess)

fig, ax = plt.subplots(figsize=(8, 8), layout="tight")
plot_solution(ax, x, exact_solution, sol.x, sol.y[0])

Практикум по компьютерным технологиям

Решение ОДУ

Contents

Решение ОДУ#

Задача Коши#

Уравнение первого порядка#

Уравнения высшего порядка#

Выбор метода решения ОДУ#

Краевая задача#